
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)求函数f(x)的极值.
【答案】(1) x+y-2=0;(2) 当a≤0时,函数f(x)无极值;当a>0时,函数f(x)在x=a处取得极小值a-aln a无极大
【解析】
解:函数f(x)的定义域为(0,+∞),f′(x)=1-![]() .
.
(1)当a=2时,f(x)=x-2ln x,
f′(x)=1-![]() (x>0),
(x>0),
因而f(1)=1,f′(1)=-1,
所以曲线y=f(x)在点A(1,f(1))处的切线方程为y-1=-(x-1),即x+y-2=0.
(2)由f′(x)=1-![]() =
=![]() ,x>0知:
,x>0知:
①当a≤0时,f′(x)>0,函数f(x)为(0,+∞)上的增函数,函数f(x)无极值;
②当a>0时,由f′(x)=0,解得x=a,
又当x∈(0,a)时,f′(x)<0;
当x∈(a,+∞)时,f′(x)>0,
从而函数f(x)在x=a处取得极小值,且极小值为f(a)=a-aln a,无极大值.
综上,当a≤0时,函数f(x)无极值;
当a>0时,函数f(x)在x=a处取得极小值a-aln a,无极大值.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
【题目】PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,空气污染越严重.PM2.5的浓度与空气质量类别的关系如下表所示:

从甲城市2016年9月份的30天中随机抽取15天,这15天的PM2.5的日均浓度指数数据如茎叶图所示.
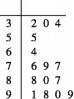
(1)试估计甲城市在2016年9月份的30天中,空气质量类别为优或良的天数;
(2)从甲城市的这15个监测数据中任取2个,设X是空气质量类别为优或良的天数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生对其亲属30人的饮食习惯进行了一次调查,并用下图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主)
(1)根据以上数据完成下面的2×2列联表:
主食 蔬菜 | 主食 肉类 | 总计 | |
50岁以下 | |||
50岁以上 | |||
总计 |
(2)能否在犯错误的概率不超过0.010的前提下认为“其亲属的饮食习惯与年龄有关”?并写出简要分析.
附参考公式:![]()
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,已知圆![]() 的圆心坐标为
的圆心坐标为![]() ,半径为
,半径为![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,直线l的参数方程为:
轴的正半轴为极轴建立极坐标系,直线l的参数方程为:![]() (
(![]() 为参数).
为参数).
(1)求圆![]() 和直线l的极坐标方程;
和直线l的极坐标方程;
(2)点![]() 的极坐标为
的极坐标为![]() ,直线l与圆
,直线l与圆![]() 相交于A,B,求
相交于A,B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},其前n项和为Sn .
(1)若{an}是公差为d(d>0)的等差数列,且{ ![]() }也为公差为d的等差数列,求数列{an}的通项公式;
}也为公差为d的等差数列,求数列{an}的通项公式;
(2)若数列{an}对任意m,n∈N* , 且m≠n,都有 ![]() =am+an+
=am+an+ ![]() ,求证:数列{an}是等差数列.
,求证:数列{an}是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+ ![]() )(ω>0)的最小正周期为π,则该函数的图象( )
)(ω>0)的最小正周期为π,则该函数的图象( )
A.关于直线x= ![]() 对称
对称
B.关于点( ![]() ,0)对称
,0)对称
C.关于直线x=﹣ ![]() 对称
对称
D.关于点( ![]() ,0)对称
,0)对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,A,B,C的对边分别是a,b,c,3sin2C+8sin2A=11sinAsinC,且c<2a.
(1)求证:△ABC为等腰三角形
(2)若△ABC的面积为8 ![]() .且sinB=
.且sinB= ![]() ,求BC边上的中线长.
,求BC边上的中线长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,武汉市出现了非常严重的雾霾天气,而燃放烟花爆竹会加重雾霾,是否应该全面禁放烟花爆竹已成为人们议论的一个话题.武汉市环保部门就是否赞成禁放烟花爆竹,对400位老年人和中青年市民进行了随机问卷调查,结果如下表:
赞成禁放 | 不赞成禁放 | 合计 | |
老年人 | 60 | 140 | 200 |
中青年人 | 80 | 120 | 200 |
合计 | 140 | 260 | 400 |
附:K2= ![]()
P(k2>k0) | 0.050 | 0.025 | 0.010 |
k0 | 3.841 | 5.024 | 6.635 |
(1)有多大的把握认为“是否赞成禁放烟花爆竹”与“年龄结构”有关?请说明理由;
(2)从上述不赞成禁放烟花爆竹的市民中按年龄结构分层抽样出13人,再从这13人中随机的挑选2人,了解他们春节期间在烟花爆竹上消费的情况.假设一位老年人花费500元,一位中青年人花费1000元,用X表示它们在烟花爆竹上消费的总费用,求X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com