
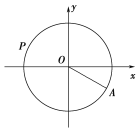
【题目】水车在古代是进行灌溉引水的工具,是人类的一项古老的发明,也是人类利用自然和改造自然的象征.如图是一个半径为R的水车,一个水斗从点A(3![]() ,-3)出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时60秒.经过t秒后,水斗旋转到P点,设P的坐标为(x,y),其纵坐标满足y=f(t)=Rsin(ωt+φ)(t≥0,ω>0,|φ|<
,-3)出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时60秒.经过t秒后,水斗旋转到P点,设P的坐标为(x,y),其纵坐标满足y=f(t)=Rsin(ωt+φ)(t≥0,ω>0,|φ|<![]() ).则下列叙述错误的是( )
).则下列叙述错误的是( )
A.R=6,ω=![]() ,φ=-
,φ=-![]()
B.当t∈[35,55]时,点P到x轴的距离的最大值为6
C.当t∈[10,25]时,函数y=f(t)单调递减
D.当t=20时,|PA|=6![]()
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AD=2.
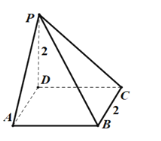
(1)求该四棱锥P-ABCD的表面积和体积;
(2)求该四棱锥P-ABCD内切球的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的一个顶点与抛物线
的一个顶点与抛物线![]() 的焦点重合,
的焦点重合,![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,其离心率
的左、右焦点,其离心率![]() 椭圆
椭圆![]() 右焦点
右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在直线![]() ,使得
,使得![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高尔顿(钉)板是在一块竖起的木板上钉上一排排互相平行、水平间隔相等的圆柱形铁钉(如图),并且每一排钉子数目都比上一排多一个,一排中各个钉子恰好对准上面一排两相邻铁钉的正中央.从入口处放入一个直径略小于两颗钉子间隔的小球,当小球从两钉之间的间隙下落时,由于碰到下一排铁钉,它将以相等的可能性向左或向右落下,接着小球再通过两铁钉的间隙,又碰到下一排铁钉.如此继续下去,在最底层的5个出口处各放置一个容器接住小球.
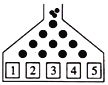
(Ⅰ)理论上,小球落入4号容器的概率是多少?
(Ⅱ)一数学兴趣小组取3个小球进行试验,设其中落入4号容器的小球个数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某市拟在长为8 km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数![]() ,
,![]() 的图象,且图象的最高点为
的图象,且图象的最高点为![]() ;赛道的后一部分为折线段MNP.为保证参赛运动员的安全,限定
;赛道的后一部分为折线段MNP.为保证参赛运动员的安全,限定![]() .
.
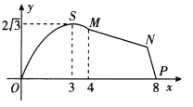
(1)求点M的坐标;
(2)应如何设计,才能使折线段赛道MNP最长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义在R上的函数![]() 满足:对于任意实数x、y,总有
满足:对于任意实数x、y,总有![]() 恒成立,我们称
恒成立,我们称![]() 为“类余弦型”函数.
为“类余弦型”函数.
![]() 已知
已知![]() 为“类余弦型”函数,且
为“类余弦型”函数,且![]() ,求
,求![]() 和
和![]() 的值;
的值;
![]() 在
在![]() 的条件下,定义数列
的条件下,定义数列![]() 2,3,
2,3,![]() 求
求![]() 的值.
的值.
![]() 若
若![]() 为“类余弦型”函数,且对于任意非零实数t,总有
为“类余弦型”函数,且对于任意非零实数t,总有![]() ,证明:函数
,证明:函数![]() 为偶函数,设有理数
为偶函数,设有理数![]() ,
,![]() 满足
满足![]() ,判断
,判断![]() 和
和![]() 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右顶点为A,上顶点为B.已知椭圆的离心率为
的右顶点为A,上顶点为B.已知椭圆的离心率为![]() ,
,![]() .
.
(1)求椭圆的方程;
(2)设直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,
两点,![]() 与直线
与直线![]() 交于点M,且点P,M均在第四象限.若
交于点M,且点P,M均在第四象限.若![]() 的面积是
的面积是![]() 面积的2倍,求
面积的2倍,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com