解:(1)f′(x)=e
x+a,把x=1代入得:f′(1)=e+a,
把x=1代入f(x)得:f(1)=e+a,所以切点坐标为(1,e+a),
则在x=1处的切线为y-(e+a)=(e+a)(x-1)即:y=(e+a)x,
与y
2=4(x-1)联立,消去得(e+a)
2x
2-4x+4=0,
由△=0知,a=1-e或a=-1-e;(4分)
(2)f′(x)=e
x+a,
①当a>0时,f′(x)>0,f(x)在R上单调递增,且当x→-∞时,e
x→0,ax→-∞,
∴f(x)→-∞,故f(x)>0不恒成立,所以a>0不合题意;(6分)
②当a=0时,f(x)=e
x>0对x∈R恒成立,所以a=0符合题意;
③当a<0时令f′(x)=e
x+a=0,得x=ln(-a),
当x∈(-∞,ln(-a))时,f′(x)<0,当x∈(ln(-a),+∞)时,f′(x)>0,
故f(x)在(-∞,ln(-a))上是单调递减,在(ln(-a),+∞)上是单调递增,
所以[f(x)]
min=f(ln(-a))=-a+aln(-a)>0,
解得a>-e,又a<0,∴a∈(-e,0),
综上:a∈(-e,0].(10分)
(3)当a=-1时,由(2)知[f(x)]
min=f(ln(-a))=-a+aln(-a)=1,
设h(x)=g(x)-f(x)=e
xlnx-e
x+x,则
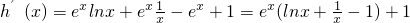
,
假设存在实数x
0∈(0,+∞),使曲线C:y=g(x)-f(x)在点x=x
0处的切线斜率与f(x)在R上的最小值相等,
x
0即为方程的解,(13分)
令h′(x)=1得:
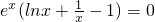
,因为e
x>0,所以
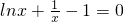
.
令
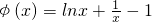
,则
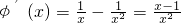
,
当0<x<1是φ′(x)<0,当x>1时φ′(x)>0,
所以
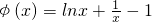
在(0,1)上单调递减,在(1,+∞)上单调递增,
∴φ(x)>φ(1)=0,故方程
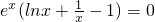
有唯一解为1,
所以存在符合条件的x
0,且仅有一个x
0=1.(16分)
分析:(1)求出f(x)的导函数,把c=1代入导函数中求出的导函数值即为切线方程的斜率,把x=1代入f(x)求出切点的纵坐标,根据切点坐标和斜率写出切线的方程,把切线方程与抛物线联立,消去y得到关于x的一元二次方程,根据直线与抛物线相切,得到方程的根的判别式等于0,列出关于a的方程,求出方程的解即可得到a的值;
(2)求出f(x)的导函数,分a大于0,a=0和a小于0三种情况考虑,当a大于0时,导函数大于0,即函数为增函数,利用极限的思想得到函数恒大于0不成立;当a=0时,得到函数恒大于0,满足题意;当a小于0时,令导函数等于0,求出x的值,由x的值分区间讨论导函数的正负,得到函数的单调区间,进而得到f(x)的最小值,让最小值大于0,列出关于a的不等式,求出不等式的解集即可得到a的取值范围,综上,得到满足题意的a的取值范围;
(3)把a=-1代入到(2)中求出的f(x)的最小值中,确定出f(x)的最小值,设h(x)=g(x)-f(x),把g(x)和f(x)的解析式代入确定出h(x),求出h(x)的导函数,假如存在x
0∈(0,+∞),使曲线C:y=g(x)-f(x)在点x=x
0处的切线斜率与f(x)在R上的最小值相等,令h(x)导函数等于f(x)的最小值,得到
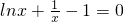
,设φ(x)等于等式的右边,求出φ(x)的导函数,利用导函数的正负确定出φ(x)的最小值为φ(1)等于0,得到方程有唯一的解,且唯一的解为f(x)的最小值.
点评:此题考查学生会利用导数求切线上过某点切线方程的斜率,会利用导函数的正负确定函数的单调区间,会利用导数研究函数的极值,掌握导数在最大值、最小值问题中的应用,是一道中档题.

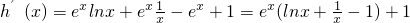 ,
,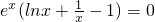 ,因为ex>0,所以
,因为ex>0,所以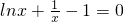 .
.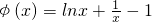 ,则
,则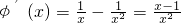 ,
,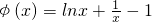 在(0,1)上单调递减,在(1,+∞)上单调递增,
在(0,1)上单调递减,在(1,+∞)上单调递增,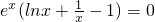 有唯一解为1,
有唯一解为1,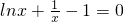 ,设φ(x)等于等式的右边,求出φ(x)的导函数,利用导函数的正负确定出φ(x)的最小值为φ(1)等于0,得到方程有唯一的解,且唯一的解为f(x)的最小值.
,设φ(x)等于等式的右边,求出φ(x)的导函数,利用导函数的正负确定出φ(x)的最小值为φ(1)等于0,得到方程有唯一的解,且唯一的解为f(x)的最小值.
