[题目]已知函数.在上为增函数.求m的取值范围,的值域为R.求m的取值范围. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知函数。

(1)若f(x)在上为增函数，求m的取值范围；

(2)若f(x)的值域为R，求m的取值范围。

【答案】（1）；（2）.

【解析】

（1）根据复合函数“同增异减”，知t=为减函数，根据对数的概念，知t=>0在(-∞,上恒成立，分类讨论，进而确定m的取值范围；

（2）由f（x）的值域为R，得t=值域为（0，+∞），结合二次函数的性质得到关于m的不等式，解不等式即可.

由题意y=可看成由y=与t=复合而成

由于f(x)在(-∞,上为增函数，根据对数函数的单调性，

所以t=在(-∞,上为减函数，且在(-∞,上恒成立

当m=0时，不符合题意；

当m>0时，要符合题意，应满足且4m-1>0,所以<m；

当m<0时，不符题意；

综上，<m；

（2）由f（x）的值域为R，t=值域为（0，+∞）

当m=0时，t=-2x+3，在x<的值域为（0，+∞），符合题意；

当m>0时，要符合题意，应满足即4-12m；

当m<0时，不符合题意。

综上，.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】己知直线2x﹣y﹣1=0与直线x﹣2y+1=0交于点P．

（Ⅰ）求过点P且平行于直线3x+4y﹣15=0的直线的方程；（结果写成直线方程的一般式）

（Ⅱ）求过点P并且在两坐标轴上截距相等的直线方程（结果写成直线方程的一般式）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】函数f（x）= x3﹣ax2﹣4在（3，+∞）上是增函数，则实数a的取值范围为

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=alnx﹣ax﹣3（a≠0）．
（1）讨论f（x）的单调性；
（2）若f（x）+（a+1）x+4﹣e≤0对任意x∈[e，e2]恒成立，求实数a的取值范围（e为自然常数）；
（3）求证ln（22+1）+ln（32+1）+ln（42+1）+…+ln（n2+1）＜1+2lnn!（n≥2，n∈N*）（n!=1×2×3×…×n）．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】备受瞩目的巴西世界杯正在如火如荼的进行，为确保总决赛的顺利进行，组委会决定在位于里约热内卢的马拉卡纳体育场外临时围建一个矩形观众候场区，总面积为72m2（如图所示）．要求矩形场地的一面利用体育场的外墙，其余三面用铁栏杆围，并且要在体育馆外墙对面留一个长度为2m的入口．现已知铁栏杆的租用费用为100元/m．设该矩形区域的长为x（单位：m），租用铁栏杆的总费用为y（单位：元）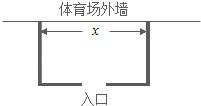

（1）将y表示为x的函数；
（2）试确定x，使得租用此区域所用铁栏杆所需费用最小，并求出最小最小费用．