【题目】已知函数
．
(Ⅰ)若
,令函数
,求函数
在
上的极大值、极小值；
(Ⅱ)若函数
在
上恒为单调递增函数,求实数
的取值范围.
科目：高中数学 来源： 题型：
【题目】国际奥委会将于2017年9月15日在秘鲁利马召开130次会议决定2024年第33届奥运
会举办地。目前德国汉堡、美国波士顿等申办城市因市民担心赛事费用超支而相继退出。某机构为调查我国公民对申办奥运会的态度，选了某小区的100位居民调查结果统计如下：
支持 | 不支持 | 合计 | |
年龄不大于50岁 | 80 | ||
年龄大于50岁 | 10 | ||
合计 | 70 | 100 |
（1）根据已有数据，把表格数据填写完整；
（2）能否在犯错误的概率不超过5％的前提下认为不同年龄与支持申办奥运无关?
（3）已知在被调查的年龄大于50岁的支持者中有5名女性，其中2位是女教师，现从这5名女性中随机抽取3人，求至多有1位教师的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
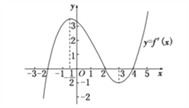
【题目】函数
的导函数的图象如图所示，给出下列判断：
①函数
在区间
内单调递增；②函数
在区间
内单调递减；③函数
在区间
内单调递增；④当
时，函数
有极小值；⑤当
时，函数
有极大值．则上述判断中正确的是( )
A. ①② B. ③
C. ②③ D. ③④⑤
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设首项为1的正项数列{an}的前n项和为Sn，且Sn＋1－3Sn＝1.
(1) 求证：数列{an}为等比数列；
(2) 数列{an}是否存在一项ak，使得ak恰好可以表示为该数列中连续r(r∈N*，r≥2)项的和？请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知三条直线l1：2x-y+a =" 0" (a＞0)，直线l2：-4x+2y+1 = 0和直线l3：x+y-1= 0，且l1与l2的距离是
．
（1）求a的值；
（2）能否找到一点P，使得P点同时满足下列三个条 件：
①P是第一象限的点；
②P 点到l1的距离是P点到l2的距离的
；
③P点到l1的距离与P点到l3的距离之比是
∶
．若能，求P点坐标；若不能，说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在
中,根据下列条件解三角形,其中有两个解的是（ ）
A. b="10," A=450, C=600 B. a=6, c=5, B=600
C. a=7, b=5, A=600 D. a=14, b="16," A=450
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】【湖南省2017届高三长郡中学、衡阳八中等十三校重点中学第一次联考数学（理）】
已知函数
.
（1）当
时，试求函数图像过点
的切线方程；
（2）当
时，若关于
的方程
有唯一实数解，试求实数
的取值范围；
（3）若函数
有两个极值点
，且不等式
恒成立，试求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，已知椭圆
： 
的离心率为
，以椭圆
的左顶点
为圆心作圆
： 
，设圆
与椭圆
交于点
与点
．
（1）求椭圆
的方程；
（2）求
的最小值，并求此时圆
的方程；
（3）设点
是椭圆
上异于
, 
的任意一点，且直线
分别与
轴交于点
， 
为坐标原点，求证： 
为定值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
