Question

一海豚在水池中自由游弋，水池为长30米，宽20米的长方形，求此海豚嘴离岸边不超过2米的概率.

(1)采用设计模拟试验的方法，估计事件A=“海豚嘴尖离岸边不超过2米”的概率;

(2)采用“几何概型”求事件的概率.

 

           

Answer 1

思路分析：本题考查随机模拟法求概率及几何概型的求法.

解：(1)用计算机产生随机数来模拟海豚在水中自由游弋的试验.先产生随机数x、y，它们表示海豚嘴尖的横坐标与纵坐标，如果(x，y)出现在图示的阴影区域，我们说事件A发生了，算法步骤如下：

    第一步：利用计算器或计算机产生-15—15之间的随机数作为海豚嘴尖的横坐标，产生-10—10之间的随机数作为海豚嘴尖的纵坐标.

    第二步：判断(x，y)是否落在阴影部分，即是否满足||x|-15|≤2或||y|-10|≤2，如果是，则事件A发生了，记录发生次数m.

    第三步：记录试验次数n，若继续试验，则返回第一步，否则程序结束.

程序结束后事件A发生的频率作为A的概率的近似值，所以P(A)≈.

下表是部分模拟的结果，供大家参考：

试验次数	事件A的次数	事件A的频率
100	35	0.35
1 000	324	0.324
10 000	2 997	0.299 7
100 000	30 506	0.305 06

(2)对于几何概型，关键是要构造出随机事件对应的几何图形，利用图形的几何度量来求随机事件的概率.

   

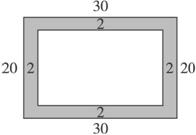
图3-3-8

 如图3-3-8所示，大矩形表示长30 m，宽20 m的水池，图中阴影部分表示事件A=“海豚嘴尖离岸边不超过2 m”，问题转化为求海豚嘴尖出现在图中阴影部分的概率.

于是事件P(A)=≈0.31.

    巧解提示 比较用模拟方法得到的事件A的概率与几何概型计算得到的事件A的概率可知，这两个结果极其相似，

    说明模拟方法是一种非常有效而且广泛使用的方法，尤其是现实的试验难以实施或不可能实施时，模拟可以给我们提供解决问题的方案.