
【题目】![]() 是指悬浮在空气中的空气动力学当量直径小于或等于
是指悬浮在空气中的空气动力学当量直径小于或等于![]() 微米的颗粒物,也称为可入肺颗粒物.根据现行国家标准
微米的颗粒物,也称为可入肺颗粒物.根据现行国家标准![]() ,
,![]() 日均值在
日均值在![]() 微克/立方米以下,空气质量为一级;在
微克/立方米以下,空气质量为一级;在![]() 微克应立方米
微克应立方米![]() 微克立方米之间,空气质量为二级:在
微克立方米之间,空气质量为二级:在![]() 微克/立方米以上,空气质量为超标.从某市
微克/立方米以上,空气质量为超标.从某市![]() 年全年每天的
年全年每天的![]() 监测数据中随机地抽取
监测数据中随机地抽取![]() 天的数据作为样本,监测值频数如下表:
天的数据作为样本,监测值频数如下表:
(微克/立方米) |
|
|
|
|
|
|
频数(天) |
|
|
|
|
|
|
(1)从这![]() 天的
天的![]() 日均值监测数据中,随机抽出
日均值监测数据中,随机抽出![]() 天,求恰有
天,求恰有![]() 天空气质量达到一级的概率;
天空气质量达到一级的概率;
(2)从这![]() 天的数据中任取
天的数据中任取![]() 天数据,记
天数据,记![]() 表示抽到
表示抽到![]() 监测数据超标的天数,求
监测数据超标的天数,求![]() 的分布列.
的分布列.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分
沙漏是古代的一种计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时。如图,某沙漏由上下两个圆锥组成,圆锥的底面直径和高均为8cm,细沙全部在上部时,其高度为圆锥高度的![]() (细管长度忽略不计).
(细管长度忽略不计).

(1)如果该沙漏每秒钟漏下0.02cm3的沙,则该沙漏的一个沙时为多少秒(精确到1秒)?
(2)细沙全部漏入下部后,恰好堆成个一盖住沙漏底部的圆锥形沙堆,求此锥形沙堆的高度(精确到0.1cm).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
:![]() 过点
过点![]() ,
,![]() ,
,![]() 为椭圆
为椭圆![]() 的左、右焦点,离心率为
的左、右焦点,离心率为![]() ,圆
,圆![]() 的直径为
的直径为![]() .
.
(1)求椭圆![]() 及圆
及圆![]() 的方程;
的方程;
(2)设直线![]() 与圆
与圆![]() 相切于第一象限内的点
相切于第一象限内的点![]() .
.
①若直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点,求点
有且只有一个公共点,求点![]() 的坐标;
的坐标;
②若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是曲线
是曲线![]() :
:![]() 上的动点,延长
上的动点,延长![]() (
(![]() 是坐标原点)到
是坐标原点)到![]() ,使得
,使得![]() ,点
,点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若点![]() ,
,![]() 分别是曲线
分别是曲线![]() 的左、右焦点,求
的左、右焦点,求![]() 的取值范围;
的取值范围;
(3)过点![]() 且不垂直
且不垂直![]() 轴的直线
轴的直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点为
的左、右焦点为![]() ,
,![]() ,长轴端点为
,长轴端点为![]() ,
,![]() ,
,![]() 为椭圆中心,
为椭圆中心,![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点,这两点在
交于不同的两点,这两点在![]() 轴上的射影恰好是椭圆
轴上的射影恰好是椭圆![]() 的两个焦点.
的两个焦点.

(1)求椭圆![]() 的方程;
的方程;
(2)若抛物线![]() 上存在两个点
上存在两个点![]() ,
,![]() ,椭圆
,椭圆![]() 上存在两个点
上存在两个点![]() ,
,![]() ,满足
,满足![]() ,
,![]() ,
,![]() 三点共线,
三点共线,![]() ,
,![]() ,
,![]() 三点共线,且
三点共线,且![]() ,求四边形
,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,平面
中,平面![]() 平面
平面![]() .四边形
.四边形![]() 为正方形,四边形
为正方形,四边形![]() 为梯形,且
为梯形,且![]() ,
,![]() 是边长为1的等边三角形,M为线段
是边长为1的等边三角形,M为线段![]() 中点,
中点,![]() .
.
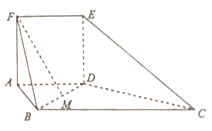
(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)线段![]() 上是否存在点N,使得直线
上是否存在点N,使得直线![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心为
的圆心为![]() ,圆内一条过点
,圆内一条过点![]() 的动弦
的动弦![]() (与
(与![]() 轴不重合),过点
轴不重合),过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() .
.
(1)求出点![]() 的轨迹方程;
的轨迹方程;
(2)若过点![]() 的直线
的直线![]() 交
交![]() 的轨迹方程于不同两点
的轨迹方程于不同两点![]() ,
,![]() ,
,![]() 为坐标原点,且
为坐标原点,且![]() ,点
,点![]() 为椭圆上一点,求点
为椭圆上一点,求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,右焦点为
,右焦点为![]() ,以原点
,以原点![]() 为圆心,椭圆
为圆心,椭圆![]() 的短半轴长为半径的圆与直线
的短半轴长为半径的圆与直线![]() 相切.
相切.

(1)求椭圆![]() 的方程;
的方程;
(2)如图,过定点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,连接
两点,连接![]() 并延长交
并延长交![]() 于
于![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com