
| A. | $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ | B. | $\frac{x^2}{4}+{y^2}=1$ | C. | ${x^2}+\frac{y^2}{4}=1$ | D. | $\frac{{x}^{2}}{2}$+$\frac{y^2}{4}$=1 |
分析 确定抛物线y2=8x的焦点坐标,双曲线${x^2}-\frac{y^2}{2}=1$的焦点坐标,可得椭圆中相应的参数,即可求得椭圆的方程.
解答 解:抛物线y2=8x的焦点坐标为(2,0),双曲线${x^2}-\frac{y^2}{2}=1$的焦点坐标为(±$\sqrt{3}$,0),
∵椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$过抛物线y2=8x的焦点,且与双曲线${x^2}-\frac{y^2}{2}=1$有相同的焦点,
∴a=2,c=$\sqrt{3}$,
∴b=1,
∴该椭圆的方程是$\frac{x^2}{4}+{y^2}=1$,
故选B.
点评 本题考查圆锥曲线的共同特征,考查学生的计算能力,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$+1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
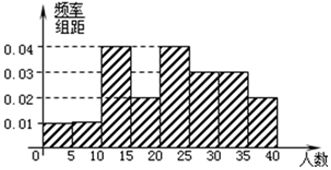
| A. | 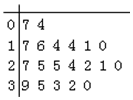 | B. | 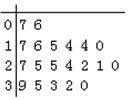 | C. | 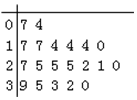 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在频率分布直方图中,众数左边和右边的直方图的面积相等 | |
| B. | 为调查高三年级的240名学生完成作业所需的时间,由教务处对高三年级的学生进行编号,从001到240抽取学号最后一位为3的学生进行调查,则这种抽样方法为分层抽样 | |
| C. | “x≠1”是“x2-3x+2≠0”的充分不必要条件 | |
| D. | 命题p:“?x0∈R,${x_0}^2-3{x_0}+2<0$”的否定为:“?x∈R,x2-3x+2≥0” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 5 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
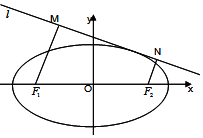 已知F1,F2 分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+y2=1,(a>1)的左、右焦点,P在椭圆上且到两个焦点F1,F2 的距离之和为2$\sqrt{2}$.
已知F1,F2 分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+y2=1,(a>1)的左、右焦点,P在椭圆上且到两个焦点F1,F2 的距离之和为2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-5,5) | B. | (5,-5) | C. | (-3,3) | D. | (3,-3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com