
【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,已知平面AA1C1C⊥平面ABCD,且 ![]() ,AD=CD=1.
,AD=CD=1.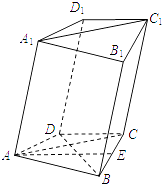
(1)求证:BD⊥AA1;
(2)若E为棱BC的中点,求证:AE∥平面DCC1D1 .
科目:高中数学 来源: 题型:
【题目】随着雾霾日益严重,很多地区都实行了“限行”政策,现从某地区居民中,随机抽取了300名居民了解他们对这一政策的态度,绘成如图所示的2×2列联表:
反对 | 支持 | 合计 | |
男性 | 70 | 60 | |
女性 | 50 | 120 | |
合计 |
(1)试问有没有99%的把握认为对“限行”政策的态度与性别有关?
(2)用样本估计总体,把频率作为概率,若从该地区所有的居民(人数很多)中随机抽取3人,用ξ表示所选3人中反对的人数,试写出ξ的分布列,并求出ξ的数学期望.
K2= ![]() ,其中n=a+b+c+d独立性检验临界表:
,其中n=a+b+c+d独立性检验临界表:
P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2lnx+x2﹣ax,a∈R.
(1)若函数y=f(x)在(0,+∞)上单调递增,求实数a的取值范围;
(2)若a=e,解不等式:f(x)<2;
(3)求证:当a>4时,函数y=f(x)只有一个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE,设PA=1,AD=2.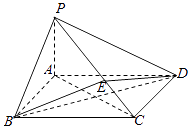
(1)求平面BPC的法向量;
(2)求二面角B﹣PC﹣A的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0).
=1(a>b>0).
(1)若椭圆的离心率为 ![]() ,且点(1,
,且点(1, ![]() )在椭圆上,
)在椭圆上,
①求椭圆的方程;
②设P(﹣1,﹣ ![]() ),R、S分别为椭圆C的右顶点和上顶点,直线PR和PS与y轴和x轴相交于点M,N,求直线MN的方程.
),R、S分别为椭圆C的右顶点和上顶点,直线PR和PS与y轴和x轴相交于点M,N,求直线MN的方程.
(2)设D(b,0),过D点的直线l与椭圆C交于E、F两点,且E、F均在y轴的右侧, ![]() =2
=2 ![]() ,求椭圆离心率的取值范围.
,求椭圆离心率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人进行羽毛球练习赛,其中两人比赛,另一人当裁判.每局比赛结束时,负的一方在下局当裁判,假设每局比赛中,甲胜乙的概率为 ![]() ,甲胜丙、乙胜丙的概率都是
,甲胜丙、乙胜丙的概率都是 ![]() ,各局比赛的结果相互独立,第一局甲当裁判.
,各局比赛的结果相互独立,第一局甲当裁判.
(1)求第3局甲当裁判的概率;
(2)记前4局中乙当裁判的次数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a0∈R,an+1=2n﹣3an , (n=0,1,2,…)
(1)设bn= ![]() ,试用a0 , n表示bn(即求数列{bn}的通项公式);
,试用a0 , n表示bn(即求数列{bn}的通项公式);
(2)求使得数列{an}递增的所有a0的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C满足sin2A+sin(A﹣B+C)=sin(C﹣A﹣B)+ ![]() ,面积S满足1≤S≤2,记a,b,c分别为A,B,C所对的边,在下列不等式一定成立的是( )
,面积S满足1≤S≤2,记a,b,c分别为A,B,C所对的边,在下列不等式一定成立的是( )
A.bc(b+c)>8
B.ab(a+b)>16 ![]()
C.6≤abc≤12
D.12≤abc≤24
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com