
【题目】若定义在R上的函数![]() ,其图像是连续不断的,且存在常数
,其图像是连续不断的,且存在常数![]() 使得
使得![]() 对任意实数x都成立,则称
对任意实数x都成立,则称![]() 是一个“k~特征函数”.则下列结论中正确命题序号为____________.
是一个“k~特征函数”.则下列结论中正确命题序号为____________.
①![]() 是一个“k~特征函数”;②
是一个“k~特征函数”;②![]() 不是“k~特征函数”;
不是“k~特征函数”;
③![]() 是常数函数中唯一的“k~特征函数”;④“
是常数函数中唯一的“k~特征函数”;④“![]() ~特征函数”至少有一个零点;
~特征函数”至少有一个零点;
【答案】①②④
【解析】
根据题意:依次检验定义域,连续性,是否存在常数![]() 使得
使得![]() 对任意实数x都成立即可.
对任意实数x都成立即可.
①![]() ,考虑
,考虑![]() 即:
即:![]() ,
,![]() ,
,
考虑![]() ,必存在
,必存在![]() 使
使![]() ,
,
即存在![]() ,使得
,使得![]() 对任意实数x都成立,所以①正确;
对任意实数x都成立,所以①正确;
②![]() ,讨论
,讨论![]() ,即
,即![]()
当![]() 时,关于
时,关于![]() 的方程
的方程![]() 无解,
无解,
不存在![]() 使
使![]() 对任意实数x都成立,
对任意实数x都成立,
所以![]() 不是“k~特征函数”,所以②正确;
不是“k~特征函数”,所以②正确;
③设常数函数![]() ,讨论
,讨论![]() ,即
,即![]() ,
,
当![]() 时对任意实数x都成立,所以任何一个常数函数都可以是“-1~特征函数”,
时对任意实数x都成立,所以任何一个常数函数都可以是“-1~特征函数”,
所以③错误;
④设![]() 是“
是“![]() ~特征函数”, 则
~特征函数”, 则![]() 是定义在R上的连续函数,
是定义在R上的连续函数,
且![]() 对任意实数x都成立,
对任意实数x都成立,
下面利用反证法证明![]() 必有零点:
必有零点:
证明:假设![]() 没有零点,因为
没有零点,因为![]() 是定义在R上的连续函数,则
是定义在R上的连续函数,则![]() 恒成立,或
恒成立,或![]() 恒成立;
恒成立;
当![]() 恒成立,则
恒成立,则![]() ,
,![]() ,与题矛盾;
,与题矛盾;
当![]() 恒成立,则
恒成立,则![]() ,
,![]() ,与题矛盾;
,与题矛盾;
所以![]() 必有零点,所以④正确.
必有零点,所以④正确.
故答案为:①②④


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为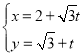 (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为
轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为![]() .
.
(1)求直线![]() 的极坐标方程及曲线C的直角坐标方程;
的极坐标方程及曲线C的直角坐标方程;
(2)若![]() 是直线
是直线![]() 上的一点,
上的一点,![]() 是曲线C上的一点,求
是曲线C上的一点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx,
(1)求函数f(x)过(﹣1,﹣2)的切线的方程
(2)过点P(1,t)存在两条直线与曲线y=f(x)相切,求t的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,
,![]() ,
,![]() 为椭圆
为椭圆![]() 上两点,圆
上两点,圆![]() .
.
(1)若![]() 轴,且满足直线
轴,且满足直线![]() 与圆
与圆![]() 相切,求圆
相切,求圆![]() 的方程;
的方程;
(2)若圆![]() 的半径为2,点
的半径为2,点![]() ,
,![]() 满足
满足![]() ,求直线
,求直线![]() 被圆
被圆![]() 截得弦长的最大值.
截得弦长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司在某市的货物转运中心,拟引进智能机器人分拣系统,以提高分拣效率和降低物流成本,已知购买x台机器人的总成本为![]() 万元.
万元.

(1)若使每台机器人的平均成本最低,问应买多少台?
(2)现按(1)中的数量购买机器人,需要安排m人将邮件放在机器人上,机器人将邮件送达指定落袋格口完成分拣(如图).经实验知,每台机器人的日平均分拣量为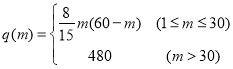 ,(单位:件).已知传统的人工分拣每人每日的平均分拣量为1200件,问引进机器人后,日平均分拣量达最大时,用人数量比引进机器人前的用人数量最多可减少百分之几?
,(单位:件).已知传统的人工分拣每人每日的平均分拣量为1200件,问引进机器人后,日平均分拣量达最大时,用人数量比引进机器人前的用人数量最多可减少百分之几?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),
为参数),![]() 为
为![]() 上的动点,
上的动点,![]() 点满足
点满足![]() ,点
,点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)在以为![]() 极点,
极点,![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() 与
与![]() 的异于极点的交点为
的异于极点的交点为![]() ,与
,与![]() 的异于极点的交点为
的异于极点的交点为![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com