
【题目】如图,在多面体![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ∥
∥![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
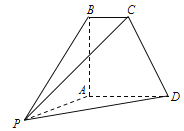
(1)求多面体![]() 的体积;
的体积;
(2)已知![]() 是棱
是棱![]() 的中点,在棱
的中点,在棱![]() 是否存在点
是否存在点![]() 使得
使得![]() ∥
∥![]() ,若存在,请确定点
,若存在,请确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
【答案】(1)![]() (2)不存在.见解析
(2)不存在.见解析
【解析】
(1)作![]() 交
交![]() 的延长线于
的延长线于![]() ,先证明
,先证明![]() 为点
为点![]() 到平面
到平面![]() 的距离,求出
的距离,求出![]() 的长度,再利用三棱锥的体积公式求多面体
的长度,再利用三棱锥的体积公式求多面体![]() 的体积;
的体积;
(2)假设棱![]() 上存在点
上存在点![]() ,使得
,使得![]() ∥
∥![]() .再证明
.再证明![]() 是
是![]() 与
与![]() 的交点
的交点![]() ,即
,即![]() 就是
就是![]() ,而
,而![]() 与
与![]() 相交,这与
相交,这与![]() ∥
∥![]() 相矛盾.即得证.
相矛盾.即得证.
解:(1)如图,

作![]() 交
交![]() 的延长线于
的延长线于![]() ,
,
因为平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,所以
,所以![]() 为点
为点![]() 到平面
到平面![]() 的距离.
的距离.
因为![]() ,
,![]() ,所以
,所以![]() ,
,
又![]() ,
,
所以![]() .
.
(2)假设棱![]() 上存在点
上存在点![]() ,使得
,使得![]() ∥
∥![]() .
.

连接![]() ,取
,取![]() 的中点
的中点![]() ,
,
在△![]() 中,因为
中,因为![]() 分别为
分别为![]() 的中点,
的中点,
所以![]() ∥
∥![]() .
.
因为过直线外一点有且只有一条直线和已知直线平行,
所以![]() 与
与![]() 重合.
重合.
因为点![]() 在线段
在线段![]() 上,
上,
所以![]() ,
,
又![]() ,
,
所以![]() 是
是![]() 与
与![]() 的交点
的交点![]() ,即
,即![]() 就是
就是![]() ,
,
而![]() 与
与![]() 相交,
相交,
这与![]() ∥
∥![]() 相矛盾,
相矛盾,
所以假设不成立,
故棱![]() 上不存在点
上不存在点![]() 使得
使得![]() ∥
∥![]() .
.


科目:高中数学 来源: 题型:
【题目】某省为迎接新高考,拟先对考生某选考学科的实际得分进行等级赋分,再按赋分后的分数从高分到低分划A、B、C、D、E五个等级,考生实际得分经赋分后的分数在到1之间.在等级赋分科学性论证时,对过去一年全省高考考生的该学科成绩重新赋分后进行分析,随机抽取2000名学生的该学科赋分后的成绩,得到如下频率分布直方图:(不考虑缺考考生的试卷)
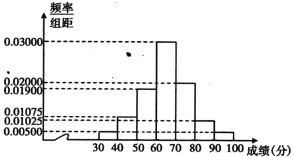
附:若X~N(μ,σ2),则P(μ-σ<X<μ+σ)=0.6826,P(μ-2σ<X<μ+2σ)=0.9544,P(μ-3σ<X<μ+3σ)=0.9974,![]() =14.59,∑(xi-
=14.59,∑(xi-![]() )2pi=213
)2pi=213
(1)求这2000名考生赋分后该学科的平均![]() (同一组中数据用该组区间中点作代表);
(同一组中数据用该组区间中点作代表);
(2)由频率分布直方图可以认为,学生经过赋分以后的成绩X服从正态分布X~N(μ,σ2),其中μ近似为样本平均数![]() ,σ2近似为样本方差s2:
,σ2近似为样本方差s2:
(i)利用正态分布,求P(50.41<X<79.59);
(ii)某市有20000名高三学生,记Y表示这20000名高三学生中赋分后该学科等级为A等(即得分大于79.59)的学生数,利用(i)的结果,求EY.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 为原点,过原点的直线(不与
为原点,过原点的直线(不与![]() 轴垂直)与椭圆
轴垂直)与椭圆![]() 交于
交于![]() 、
、![]() 两点,直线
两点,直线![]() 、
、![]() 与
与![]() 轴分别交于点
轴分别交于点![]() 、
、![]() .问:
.问:![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() ?若存在,求点
?若存在,求点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年世界读书日,陈老师给全班同学开了一份书单,推荐同学们阅读,并在2020年世界读书日时交流读书心得.经了解,甲、乙两同学阅读书单中的书本有如下信息:
①甲同学还剩![]() 的书本未阅读;
的书本未阅读;
②乙同学还剩5本未阅读;
③有![]() 的书本甲、乙两同学都没阅读.
的书本甲、乙两同学都没阅读.
则甲、乙两同学已阅读的相同的书本有( )
A.2本B.4本C.6本D.8本
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(在花卉进行硬枝扦插过程中,常需要用生根粉调节植物根系生长.现有20株使用了生根粉的花卉,在对最终“花卉存活”和“花卉死亡”进行统计的同时,也对在使用生根粉2个小时后的生根量进行了统计,这20株花卉生根量如下表所示,其中生根量在6根以下的视为“不足量”,大于等于6根为“足量”.现对该20株花卉样本进行统计,其中“花卉存活”的13株.已知“花卉存活”但生根量“不足量”的植株共1株.
编号 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
生根量 | 6 | 8 | 3 | 8 | 9 | 5 | 6 | 6 | 2 | 7 | 7 | 5 | 9 | 6 | 7 | 8 | 8 | 4 | 6 | 9 |
(1)完成![]() 列联表,并判断是否可以在犯错误概率不超过1%的前提下,认为“花卉的存活”与“生根足量”有关?
列联表,并判断是否可以在犯错误概率不超过1%的前提下,认为“花卉的存活”与“生根足量”有关?
生根足量 | 生根不足量 | 总计 | |
花卉存活 | |||
花卉死亡 | |||
总计 | 20 |
(2)若在该样本“生根不足量”的植株中随机抽取3株,求这3株中恰有1株“花卉存活”的概率.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
独立性检验中的 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学中有许多形状优美、寓意美好的曲线,如下图就是在平面直角坐标系的“心形曲线”,又名RC心形线.如果以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,其RC心形线的极坐标方程为
轴正半轴为极轴,建立极坐标系,其RC心形线的极坐标方程为![]() .
.
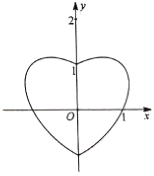
(1)求RC心形线的直角坐标方程;
(2)已知![]() 与直线
与直线![]() (
(![]() 为参数),若直线
为参数),若直线![]() 与RC心形线交于两点
与RC心形线交于两点![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国农业银行广元分行发行“金穗广元·剑门关旅游卡”是以“游广元、知广元、爱广元共享和谐广元”为主题活动的一项经济性和公益性相结合的重大举措,以最优惠的价格惠及广元户籍市民、浙江及黑龙江授建省群众、省内援建市市民,凡上述对象均可办理此卡,本人凭此卡及本人身份证一年内(期满后可重新充值办理)在广元市范围内可无限次游览所有售门票景区景点,如:剑门关、朝天明月峡、旺苍鼓城山—七里峡、青川唐家河、广元皇泽寺、苍溪梨博园、昭化古城等,现有浙江及黑龙江援建省群众甲乙两人到广元旅游(同游),第一天他们游览了剑门关、朝天明月峡,第二天他们准备从上面剩下的5个景点中选两个景点游览,则第二天游览青川唐家河的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新生儿某疾病要接种三次疫苗免疫(即0、1、6月龄),假设每次接种之间互不影响,每人每次接种成功的概率相等为了解新生儿该疾病疫苗接种剂量与接种成功之间的关系,现进行了两种接种方案的临床试验:10μg/次剂量组与20μg/次剂量组,试验结果如下:
接种成功 | 接种不成功 | 总计(人) | |
10μg/次剂量组 | 900 | 100 | 1000 |
20μg/次剂量组 | 973 | 27 | 1000 |
总计(人) | 1873 | 127 | 2000 |
(1)根据数据说明哪种方案接种效果好?并判断能否有99.9%的把握认为该疾病疫苗接种成功与两种接种方案有关?
(2)以频率代替概率,若选用接种效果好的方案,参与该试验的1000人的成功人数比此剂量只接种一次的成功人数平均提高多少人.
参考公式: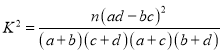 ,其中
,其中![]()
参考附表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com