
【题目】数列![]() 满足
满足![]() ,
, .
.
(1)设![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列![]() 的前n项和为
的前n项和为![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】(1)由已知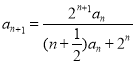 ,得
,得 ,
,
即![]() ,即
,即![]() ,即
,即![]() .(2分)
.(2分)
所以![]() ,
,![]() ,…,
,…,![]() ,
,
以上各式相加得![]() .
.
又![]() ,所以
,所以![]() .(5分)
.(5分)
(2)由(1)知![]() ,所以
,所以![]() ,
,
![]()
![]()
![]()
![]() .(7分)
.(7分)
所以![]()
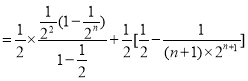
![]()
![]() .(10分)
.(10分)
【易错提醒】(1)对递推式变形时,应明确方向,准确把握数列的递推关系,通过变形将其转化为常见的等差、等比数列问题求解是解决此类问题的基本思路;(2)构造新数列时,一定要注意原数列的项与新数列的项之间的对应,如本题中第(1)问,![]() ,则
,则![]() 的表达式既不是
的表达式既不是![]() ,也不是
,也不是![]() ,而是
,而是![]() ,即把式子中所有的
,即把式子中所有的![]() 都换成
都换成![]() .
.
【解题技巧】求解数列递推关系式问题的基本原则就是对数列的递推式进行变换,把原问题转换为等差、等比数列进行处理.转化的常用方法有:(1)待定系数法,如![]() ,可以通过待定系数
,可以通过待定系数![]() 将其转化为形如
将其转化为形如![]() 的等比数列;(2)取倒数法,如本题;(3)观察变换法,如
的等比数列;(2)取倒数法,如本题;(3)观察变换法,如![]() ,可以在两端同时除以
,可以在两端同时除以![]() ,转化为形如
,转化为形如![]() 的等差数列;(4)取对数法等.求解数列递推关系式问题要注意选取合适的变换递推式的方法,通过变换进行解答,在变换时要小心谨慎.
的等差数列;(4)取对数法等.求解数列递推关系式问题要注意选取合适的变换递推式的方法,通过变换进行解答,在变换时要小心谨慎.


科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,且
,且![]() 平面
平面![]() .
.
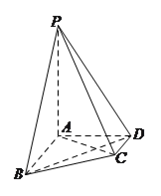
(1)设平面![]() 平面
平面![]() ,求证:
,求证: ![]() .
.
(2)求证: ![]() .
.
(3)设点![]() 为线段
为线段![]() 上一点,且直线
上一点,且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于![]() ,若数列
,若数列![]() 满足
满足![]() ,则称这个数列为“K数列”.
,则称这个数列为“K数列”.
(Ⅰ)已知数列:1,m+1,m2是“K数列”,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)是否存在首项为-1的等差数列![]() 为“K数列”,且其前n项和
为“K数列”,且其前n项和![]() 满足
满足
![]() ?若存在,求出
?若存在,求出![]() 的通项公式;若不存在,请说明理由;
的通项公式;若不存在,请说明理由;
(Ⅲ)已知各项均为正整数的等比数列![]() 是“K数列”,数列
是“K数列”,数列![]() 不是“K数列”,若
不是“K数列”,若![]() ,试判断数列
,试判断数列![]() 是否为“K数列”,并说明理由.
是否为“K数列”,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆![]() 的圆心在
的圆心在![]() 轴上,并且过
轴上,并且过![]() 两点.
两点.
(1)求圆![]() 的方程;
的方程;
(2)设直线![]() 与圆
与圆![]() 交于
交于![]() 两点,那么以
两点,那么以![]() 为直径的圆能否经过原点,若能,请求出直线
为直径的圆能否经过原点,若能,请求出直线![]() 的方程;若不能,请说明理由.
的方程;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)
某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨;生产每吨乙产品要用A原料1吨,B原料3吨,销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元.该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨.那么在一个生产周期内该企业生产甲、乙两种产品各多少吨可获得最大利润,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)
(2017天津)电视台播放甲、乙两套连续剧,每次播放连续剧时,需要播放广告.已知每次播放甲、乙两套连续剧时,连续剧播放时长、广告播放时长、收视人次如下表所示:
连续剧播放时长(分钟) | 广告播放时长(分钟) | 收视人次(万) | |
甲 | 70 | 5 | 60 |
乙 | 60 | 5 | 25 |
已知电视台每周安排的甲、乙连续剧的总播放时间不多于600分钟,广告的总播放时间不少于30分钟,且甲连续剧播放的次数不多于乙连续剧播放次数的2倍.分别用![]() ,
,![]() 表示每周计划播出的甲、乙两套连续剧的次数.
表示每周计划播出的甲、乙两套连续剧的次数.
(1)用![]() ,
,![]() 列出满足题目条件的数学关系式,并画出相应的平面区域;
列出满足题目条件的数学关系式,并画出相应的平面区域;
(2)问电视台每周播出甲、乙两套连续剧各多少次,才能使收视人次最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,且椭圆上任意一点到左焦点的最大距离为
,且椭圆上任意一点到左焦点的最大距离为![]() ,最小距离为
,最小距离为![]() .
.
(1)求椭圆的方程;
(2)过点![]() 的动直线
的动直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,试问:在坐标平面上是否存在一个定点
两点,试问:在坐标平面上是否存在一个定点![]() ,使得以线段
,使得以线段![]() 为直径的圆恒过点
为直径的圆恒过点![]() ?若存在,求出点
?若存在,求出点![]() 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”中,选出适当的一种填空:
(1)记集合A={-1,p,2},B={2,3},则“p=3”是“A∩B=B”的__________________;
(2)“a=1”是“函数f(x)=|2x-a|在区间![]() 上为增函数”的________________.
上为增函数”的________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com