
【题目】在直角坐标系xOy中,曲线C1的参数方程为 ![]() (其中α为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ. (Ⅰ)若A,B为曲线C1 , C2的公共点,求直线AB的斜率;
(其中α为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ. (Ⅰ)若A,B为曲线C1 , C2的公共点,求直线AB的斜率;
(Ⅱ)若A,B分别为曲线C1 , C2上的动点,当|AB|取最大值时,求△AOB的面积.
【答案】解:(Ⅰ)消去参数α得曲线C1的普通方程C1:x2+y2﹣2x=0.…(1) 将曲线C2:ρ=4sinθ化为直角坐标方程得x2+y2﹣4y=0.…(2)
由(1)﹣(2)得4y﹣2x=0,即为直线AB的方程,故直线AB的斜率为 ![]() ;
;
(Ⅱ)由C1:(x﹣1)2+y2=1知曲线C1是以C1(1,0)为圆心,半径为1的圆,
由C2:x2+(y﹣2)2=4知曲线C2:是以C2(0,2)为圆心,半径为2的圆.
∵|AB|≤|AC1|+|C1C2|+|BC2|,
∴当|AB|取最大值时,圆心C1 , C2在直线AB上,
∴直线AB(即直线C1C2)的方程为:2x+y=2.
∵O到直线AB的距离为 ![]() ,
,
又此时|AB|=|C1C2|+1+2=3+ ![]() ,
,
∴△AOB的面积为 ![]()
【解析】(Ⅰ)消去参数α得曲线C1的普通方程,将曲线C2化为直角坐标方程,两式作差得直线AB的方程,则直线AB的斜率可求;(Ⅱ)由C1方程可知曲线是以C1(1,0)为圆心,半径为1的圆,由C2方程可知曲线是以C2(0,2)为圆心,半径为2的圆,又|AB|≤|AC1|+|C1C2|+|BC2|,可知当|AB|取最大值时,圆心C1 , C2在直线AB上,进一步求出直线AB(即直线C1C2)的方程,再求出O到直线AB的距离,则△AOB的面积可求.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.命题p:“ ![]() ”,则?p是真命题
”,则?p是真命题
B.命题“?x∈R使得x2+2x+3<0”的否定是:“?x∈R,x2+2x+3>0”
C.“x=﹣1”是“x2+2x+3=0”的必要不充分条件
D.“a>1”是“f(x)=logax(a>0,a≠1)在(0,+∞)上为增函数”的充要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣lnx,a∈R.
(1)当a=1时,求函数f(x)在点 (1,f(1))处的切线方程;
(2)是否存在实数a,使f(x)的最小值为 ![]() ,若存在,求出a的值;若不存在,请说明理由;
,若存在,求出a的值;若不存在,请说明理由;
(3)当x∈(0,+∞)时,求证:e2x3﹣2x>2(x+1)lnx.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ln(x﹣1)+ax2+x+1,g(x)=(x﹣1)ex+ax2 , a∈R. (Ⅰ)当a=1时,求函数f(x)在点(2,f(2))处的切线方程;
(Ⅱ)若函数g(x)有两个零点,试求a的取值范围;
(Ⅲ)证明f(x)≤g(x)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,角A,B,C的对边分别是a,b,c且满足(2a﹣c)cosB=bcosC.
(1)求角B的大小;
(2)若△ABC的面积为 ![]() ,求a+c的值.
,求a+c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥P﹣ABC中,底面ABC是边长为6的正三角形,PA⊥底面ABC,且PB与底面ABC所成的角为 ![]() .
. 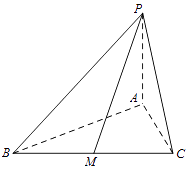
(1)求三棱锥P﹣ABC的体积;
(2)若M是BC的中点,求异面直线PM与AB所成角的大小(结果用反三角函数值表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设向量 ![]() =(a1 , a2),
=(a1 , a2), ![]() =(b1 , b2),定义一种向量运算
=(b1 , b2),定义一种向量运算 ![]()
![]() =(a1b1 , a2b2),已知向量
=(a1b1 , a2b2),已知向量 ![]() =(2,
=(2, ![]() ),
), ![]() =(
=( ![]() ,0),点P(x′,y′)在y=sinx的图象上运动.点Q(x,y)是函数y=f(x)图象上的动点,且满足
,0),点P(x′,y′)在y=sinx的图象上运动.点Q(x,y)是函数y=f(x)图象上的动点,且满足 ![]() +n(其中O为坐标原点),则函数y=f(x)的值域是( )
+n(其中O为坐标原点),则函数y=f(x)的值域是( )
A.[﹣ ![]() ,
, ![]() ]
]
B.![]()
C.[﹣1,1]
D.(﹣1,1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com