
����Ŀ���й��������ǵ���ϵͳ���й��������Ƶ�ȫ�����ǵ���ϵͳ����Ϊ����ս���Կռ������ʩ���ҹ��������ǵ���ϵͳ�����Թ�����ȫ�����ش�������������ľ���Ӧ��ҲԽ��Խ�㷺.��ͳ�ƣ�2016�����ǵ�����λ�÷����ҵ�ܲ�ֵ�ﵽ2118��Ԫ����2015��Լ����![]() .������40�����б������ǵ���ϵͳ��λ�÷����ҵ�IJ�ֵ����λ����Ԫ����Ƶ�ʷֲ�ֱ��ͼ��
.������40�����б������ǵ���ϵͳ��λ�÷����ҵ�IJ�ֵ����λ����Ԫ����Ƶ�ʷֲ�ֱ��ͼ��
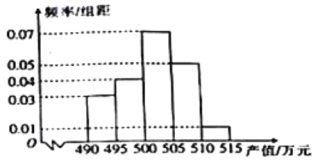
��1������Ƶ�ʷֲ�ֱ��ͼ�����ֵС��500��Ԫ�ij��и�����
��2����������ȡ��40����������ȡ2������![]() Ϊ��ֵ������500��Ԫ�ij��и�������
Ϊ��ֵ������500��Ԫ�ij��и�������![]() �ķֲ��м������ͷ���.
�ķֲ��м������ͷ���.
���𰸡�(1)14��(2)�𰸼�����.
����������������1������Ƶ�ʷֲ�ֱ��ͼ���������ֵС��500��Ԫ�ij��и�����
��2����Y�����п���ȡֵΪ0��1��2���ֱ������Ӧ�ĸ��ʣ��ɴ������![]() �ķֲ��м������ͷ���.
�ķֲ��м������ͷ���.
��⣺��1������Ƶ�ʷֲ�ֱ��ͼ��֪����ֵС��500��Ԫ�ij��и���Ϊ��[��0.03+0.04����5]��40=14��
��2��Y�����п���ȡֵΪ0��1��2��
 ��
��
 ��
��
 ��
��
��Y�ķֲ���Ϊ��
Y | 0 | 1 | 2 |
P |
|
|
|
������![]() ��
��
������![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾Ϊȷ����һ���Ͷ��ij�ֲ�Ʒ�������ѣ����˽���������![]() ����λ��ǧԪ������������
����λ��ǧԪ������������![]() ����λ��
�����![]() ����������
����������![]() ����λ��ǧԪ����Ӱ�죬�Խ�8�����������
����λ��ǧԪ����Ӱ�죬�Խ�8�����������![]() ����������
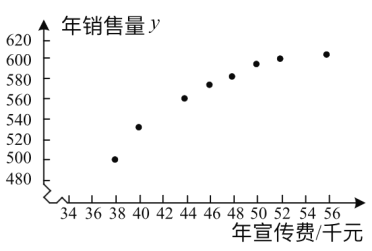
����������![]() �������˳����������õ������ɢ��ͼ��һЩͳ������ֵ.
�������˳����������õ������ɢ��ͼ��һЩͳ������ֵ.
|
|
|
|
|
|
|
46.6 | 563 | 6.8 | 298.8 | 1.6 | 1469 | 108.8 |
����![]() ��
��![]()
��1������ɢ��ͼ�жϣ�![]() ��
��![]() ��һ��������Ϊ��������
��һ��������Ϊ��������![]() ������������
������������![]() �Ļع鷽�����ͣ��������жϼ��ɣ�����˵�����ɣ�
�Ļع鷽�����ͣ��������жϼ��ɣ�����˵�����ɣ�
��2�����ݣ�1�����жϽ�����������ݣ�����![]() ����
����![]() �Ļع鷽�̣�
�Ļع鷽�̣�
��3����֪���ֲ�Ʒ��������![]() ��
��![]() ��
��![]() �Ĺ�ϵΪ
�Ĺ�ϵΪ![]() .���ݣ�2���Ľ������������
.���ݣ�2���Ľ������������![]() ʱ�������������������Ԥ��ֵ�Ƕ��٣�
ʱ�������������������Ԥ��ֵ�Ƕ��٣�
��������һ������![]() ��
��![]() ����
����![]() ����ع���
����ع���![]() ��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ��
��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ�� ��
��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABCD�У�����PAB�͵���ABCD���ҡ�PAB=��ABC=90�㣬AD��BC��PA=AB=BC=2AD��E��PC���е㣮
������֤��DE��ƽ��PBC��
����������A��PD��E������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��һ�꼶����![]() ����ѡ�Σ�ÿλͬѧ��˴˶����ش���ѡ�����ſγ̣���֪��ͬѧ��ѡ
����ѡ�Σ�ÿλͬѧ��˴˶����ش���ѡ�����ſγ̣���֪��ͬѧ��ѡ![]() �γ̣���ͬѧ��ѡ
�γ̣���ͬѧ��ѡ![]() �γ̣���ͬѧ�����ſγ��������ѡ����.
�γ̣���ͬѧ�����ſγ��������ѡ����.
��1�����ͬѧ����ͬѧǡ��һ�ſγ���ͬ�ĸ��ʣ�
��2����![]() Ϊ�ס��ҡ�����λͬѧ��ѡ
Ϊ�ס��ҡ�����λͬѧ��ѡ![]() �γ̵���������
�γ̵���������![]() �ķֲ��м���ѧ����.
�ķֲ��м���ѧ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڳ�����![]() �У�
��![]() ����
����![]() Ϊ
Ϊ![]() ���е㣮
���е㣮
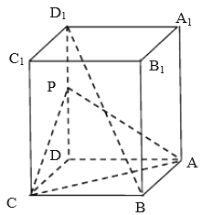
��1����֤��ֱ��![]() ƽ��
ƽ��![]() ��
��
��2����֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
��3����ֱ��![]() ��ƽ��
��ƽ��![]() �ļнǣ�
�ļнǣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1��������![]() ��ͼ���ڵ�
��ͼ���ڵ�![]() �������߷���Ϊ
�������߷���Ϊ![]() ����
����![]() ��
��![]() ��ֵ��
��ֵ��
��2����![]() ʱ��������
ʱ��������![]() �����ٴ���һ��
�����ٴ���һ��![]() ��ʹ��
��ʹ��![]() ��������ʵ��
��������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]()
��1����![]() �ĵ������䣻
�ĵ������䣻
��2����![]() Ϊ�������ҵ�
Ϊ�������ҵ�![]() ʱ��
ʱ�� ![]() �����������
�����������![]() Ϊ
Ϊ![]() �ĵ���������
�ĵ���������![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() �IJ���ͼ����ͼ��ʾ.
�IJ���ͼ����ͼ��ʾ.

��1������![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����ͼ��![]() ��ֵ������
��ֵ������![]() �ĵ����ݼ����䣻
�ĵ����ݼ����䣻
��3������![]() ��ͼ������ƽ��
��ͼ������ƽ��![]() ����λ�õ�
����λ�õ�![]() ��ͼ�����ֱ��
��ͼ�����ֱ��![]() �Գƣ���
�Գƣ���![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��B��CΪ��O�����㣬BΪ ![]() ���е㣬PΪAC�ӳ�����һ�㣬PQ���O�����ڵ�Q��BQ��AC�ཻ�ڵ�D��
���е㣬PΪAC�ӳ�����һ�㣬PQ���O�����ڵ�Q��BQ��AC�ཻ�ڵ�D��
����֤������DPQΪ���������Σ�
������PC=1��AD=PD����BDQD��ֵ��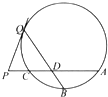
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com