
【题目】已知函数f(x)=|2x-1|+|x-2a|.
(1)当a=1时,求f(x)≤3的解集;
(2)当x∈[1,2]时,f(x)≤3恒成立,求实数a的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据绝对值定义将不等式化为三个不等式组,分别求解,最后求并集;(2)根据x∈[1,2]得|2x-1|=2x-1,再去绝对值分离变量,最后根据函数最值得实数a的取值范围.
(1)当a=1时,由f(x)≤3,可得|2x-1|+|x-2|≤3,
∴①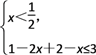 或②
或②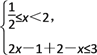 或③
或③![]()
解①得0≤x<![]() ,解②得
,解②得![]() ≤x<2,解③得x=2.
≤x<2,解③得x=2.
综上可得,0≤x≤2,即不等式的解集为[0,2].
(2)∵当x∈[1,2]时,f(x)≤3恒成立,
即|x-2a|≤3-|2x-1|=4-2x,
故2x-4≤2a-x≤4-2x,
即3x-4≤2a≤4-x.
再根据3x-4在x∈[1,2]上的最大值为6-4=2,4-x的最小值为4-2=2,
∴2a=2,∴a=1,
即a的取值范围为{1}.


科目:高中数学 来源: 题型:
【题目】对于定义在![]() 上的函数
上的函数![]() ,若存在距离为
,若存在距离为![]() 的两条直线
的两条直线![]() 和
和![]() ,使得对任意
,使得对任意![]() 都有
都有![]() 恒成立,则称函数
恒成立,则称函数![]() 有一个宽度为
有一个宽度为![]() 的通道.给出下列函数:
的通道.给出下列函数:
①![]() ; ②
; ②![]() ; ③
; ③![]() ; ④
; ④![]() .
.
其中在区间![]() 上有一个通道宽度为
上有一个通道宽度为![]() 的函数是__________(写出所有正确的序号).
的函数是__________(写出所有正确的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解七班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
喜爱打篮球 | 不喜爱打篮球 | 合 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为![]() .
.
(1)请将上面的列联表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由;
(3)现从女生中抽取2人进一步调查,设其中喜爱打篮球的女生人数为![]() ,求
,求![]() 的分布列与期望.
的分布列与期望.
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05[ | 0.025 | 0.01 | 0.005 | 0.001 |
| 2.072 | 2.70 | 3.841 | 5.024 | 6.635 | 7.879 | 10.82 |
(参考公式: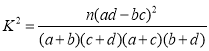 ,其中
,其中![]() )
)![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据统计,某市骑行过共享单车的人数约占全市的80%,为确定单车的投放数量以及对同年龄的车型配比,需要对该市市民每月骑行单车的次数进行统计,如表所示是对该市随机抽取100位市民的调查结果,每月骑行次数不超过20次称“不经常骑行”,超过20次称“经常骑行”.
经常骑行 | 不经常骑行 | 合计 | |
年龄不低于40岁 | 15 | 25 | 40 |
年龄低于40岁 | 35 | 25 | 60 |
合计 | 50 | 50 | 100 |
(1)是否有95%的把握认为骑行单车次数与年龄有关?
(2)以样本的频率为概率
①现从该市市民中随机抽取1人,求该人为“经常骑行”的概率
②已知该市人口约为600万,忽略把经常骑行人数的骑行次数,统计得经常骑行人群每人每月骑行次数的平均值为45次(每月按30天计算),若每辆单车每天被骑行(15次左右,可达到既缓解交通压力又减少了胡乱放置的目的,则该市配置单车的数量应为多少?
附参考公式及数据![]()
| 0.10 | 0.050 | 0.010 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个平面垂直,下列命题中错误的是( )
A.两个平面内分别垂直于交线的两条直线相互垂直
B.一个平面内的任一条直线必垂直于另一个平面.
C.一个平面内存在直线垂直于另一个平面
D.一个平面内的任意一条直线都垂直于另一个平面内的无数条直线
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖南)如下图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E、F分别是BC、CC1的中点.
(1)证明:平面AEF⊥平面B1BCC1;
(2)若直线A1C与平面A1ABB1所成的角为45°,求三棱锥F-AEC的体积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com