
【题目】化为推出一款6寸大屏手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如下:
女性用户:
分值区间 |
|
|
|
|
|
频数 | 20 | 40 | 80 | 50 | 10 |
分值区间 |
|
|
|
|
|
频数 | 45 | 75 | 90 | 60 | 30 |
男性用户:
(1)如果评分不低于70分,就表示该用户对手机“认可”,否则就表示“不认可”,完成下列![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为性别对手机的“认可”有关:
的把握认为性别对手机的“认可”有关:
女性用户 | 男性用户 | 合计 | |
“认可”手机 | |||
“不认可”手机 | |||
合计 |
附:
| 0.05 | 0.01 |
| 3.841 | 6635 |
![]()
(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取3名用户,求3名用户中评分小于90分的人数的分布列和数学期望.
【答案】(1)列联表
女性用户 | 男性用户 | 合计 | |
“认可”手机 | 140 | 180 | 320 |
“不认可”手机 | 60 | 120 | 180 |
合计 | 200 | 300 | 500 |
有![]() 的把握认为性别和对手机的“认可”有关.
的把握认为性别和对手机的“认可”有关.
(2)概率分布列为
|
|
|
|
|
|
|
|
其期望为![]() .
.
【解析】
试题分析:(1)从频数分布表算出女性用户中“认可”手机人数与“不认可”手机人数,填入表格,同理算出男性用户中“认可”手机人数与“不认可”手机人数,填入表格可得![]() 列联表,由公式计算出
列联表,由公式计算出![]() 的值与临界值中数据比较即可;(2)由分层抽样的原则算出从男性用户中抽取20名用户,评分不低于80分的人数,及评分小于90分的人数,评分不小于90分的人数,由古典概型公式分别计算
的值与临界值中数据比较即可;(2)由分层抽样的原则算出从男性用户中抽取20名用户,评分不低于80分的人数,及评分小于90分的人数,评分不小于90分的人数,由古典概型公式分别计算![]() 时的概率可列出概率分布列与期望.
时的概率可列出概率分布列与期望.
试题解析: (1)由频数分布表可得![]() 列联表如下图:
列联表如下图:
女性用户 | 男性用户 | 合计 | |
“认可”手机 | 140 | 180 | 320 |
“不认可”手机 | 60 | 120 | 180 |
合计 | 200 | 300 | 500 |
![]() ,所以有
,所以有![]() 的把握认为性别和对手机的“认可”有关.
的把握认为性别和对手机的“认可”有关.
(2)运用分层抽样从男性用户中抽取20名用户,评分不低于80分有6人,其中评分小于90分的人数为4,记为![]() ,
,![]() ,
,![]() ,
,![]() ,评分不小于90分的人数为2,记为
,评分不小于90分的人数为2,记为![]() ,
,![]() ,从6人中任取
,从6人中任取![]() 人, 评分小于90分的人数
人, 评分小于90分的人数![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,所以3名用户中评分小于90分的人数的概率分布列为
,所以3名用户中评分小于90分的人数的概率分布列为
|
|
|
|
|
|
|
|
其期望为![]() .
.


 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:
【题目】如图,椭圆![]()
![]() (
(![]() )的离心率是
)的离心率是![]() ,过点
,过点![]() (
(![]() ,
,![]() )的动直线
)的动直线![]() 与椭圆相交于
与椭圆相交于![]() ,
,![]() 两点,当直线
两点,当直线![]() 平行于
平行于![]() 轴时,直线
轴时,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
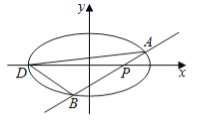
⑴求椭圆![]() 的方程:
的方程:
⑵已知![]() 为椭圆的左端点,问: 是否存在直线
为椭圆的左端点,问: 是否存在直线![]() 使得
使得![]() 的面积为
的面积为![]() ?若不存在,说明理由,若存在,求出直线
?若不存在,说明理由,若存在,求出直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,长轴在
的中心在坐标原点,长轴在![]() 轴上,
轴上,![]() 分别在其左、右焦点,
分别在其左、右焦点,![]() 在椭圆上任意一点,且
在椭圆上任意一点,且![]() 的最大值为1,最小值为
的最大值为1,最小值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆
为椭圆![]() 的右顶点,直线
的右顶点,直线![]() 是与椭圆交于
是与椭圆交于![]() 两点的任意一条直线,若
两点的任意一条直线,若![]() ,证明直线
,证明直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次水下科研考察活动中,需要潜水员潜入水深为60米的水底进行作业,根据已往经验,潜水员下潜的平均速度为![]() (米/单位时间),每单位时间的用氧量为
(米/单位时间),每单位时间的用氧量为![]() (升),在水底作业10个单位时间,每单位时间用氧量为
(升),在水底作业10个单位时间,每单位时间用氧量为![]() (升),返回水面的平均速度为
(升),返回水面的平均速度为![]() (米/单位时间),每单位时间用氧量为
(米/单位时间),每单位时间用氧量为![]() (升),记该潜水员在此次考察活动中的总用氧量为
(升),记该潜水员在此次考察活动中的总用氧量为![]() (升).
(升).
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若![]() ,求当下潜速度
,求当下潜速度![]() 取什么值时,总用氧量最少.
取什么值时,总用氧量最少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等式:sin25°+cos235°+sin 5°cos 35°=![]() ,
,
sin215°+cos245°+sin 15°cos 45°=![]() ,sin230°+cos260°+sin 30°·cos 60°=
,sin230°+cos260°+sin 30°·cos 60°=![]() ,…,由此归纳出对任意角度θ都成立的一个等式,并予以证明.
,…,由此归纳出对任意角度θ都成立的一个等式,并予以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com