
【题目】已知抛物线C:y2=2px(p>0)与圆![]() 无公共点,过抛物线C上一点M作圆D的两条切线,切点分别为E,F,当点M在抛物线C上运动时,直线EF都不通过的点构成一个区域,求这个区域的面积的取值范围.
无公共点,过抛物线C上一点M作圆D的两条切线,切点分别为E,F,当点M在抛物线C上运动时,直线EF都不通过的点构成一个区域,求这个区域的面积的取值范围.
【答案】(0,π)
【解析】
联立圆的方程和抛物线方程,可得![]() 的方程,由方程有非负数解,可得
的方程,由方程有非负数解,可得![]() ,由
,由![]() ,
,![]() 既在圆
既在圆![]() 上,又在以
上,又在以![]() 为直径的圆上,可得切点弦
为直径的圆上,可得切点弦![]() 的方程,考虑关于
的方程,考虑关于![]() 的方程有解,可得当
的方程有解,可得当![]() 运动时,直线
运动时,直线![]() 都不通过的点构成一个区域是圆
都不通过的点构成一个区域是圆![]() ,由圆的面积公式可得范围.
,由圆的面积公式可得范围.
解:抛物线![]() 与圆
与圆![]() 无公共点,
无公共点,
可得![]() 即
即![]() 无非负数解,
无非负数解,
即有△![]() ,解得
,解得![]() 或
或![]() ,
,
可得![]() ,
,![]() 设
设![]() ,
,![]() 总在圆
总在圆![]() 外部,即
外部,即![]() 对一切实数
对一切实数![]() 都成立,
都成立,
由![]() ,即
,即![]() ,即
,即![]() 成立,
成立,
点![]() ,
,![]() 在圆
在圆![]() 上,也在以
上,也在以![]() ,
,![]() ,
,![]() ,
,![]() 为直径的圆上.
为直径的圆上.
即在![]() 上,
上,
上面两个圆的方程相减可得:![]() ,
,
即为直线![]() 的方程,化为
的方程,化为![]() ,
,![]() ,
,
关于![]() 的二次方程有实数根,
的二次方程有实数根,
![]()
![]() ,
,
即![]() ,
,
即直线![]() 不经过圆
不经过圆![]() 的内部的每一个点.
的内部的每一个点.
当![]() 运动时,直线
运动时,直线![]() 都不通过的点构成一个区域是圆
都不通过的点构成一个区域是圆![]() ,
,
这个区域的面积是 ,
,
取值范围是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知动圆C过定点F(2,0),且与直线x=-2相切,圆心C的轨迹为E,
(1)求圆心C的轨迹E的方程;
(2)若直线l交E与P,Q两点,且线段PQ的中心点坐标(1,1),求|PQ|.
查看答案和解析>>
科目:高中数学 来源: 题型:
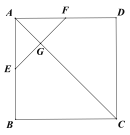
【题目】如图,正方形![]() 的边长为2,
的边长为2,![]() ,
,![]() 分别为
分别为![]() 的中点,
的中点,![]() 与
与![]() 交于点
交于点![]() ,将
,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使平面
的位置,使平面![]() 平面
平面![]() .
.

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)判断线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过抛物线y2=2px(p>0)的焦点F的直线与抛物线交于A,B两点,且![]() 3
3![]() ,抛物线的准线l与x轴交与点C,AA1垂直l于点A1,若四边形AA1CF的面积为
,抛物线的准线l与x轴交与点C,AA1垂直l于点A1,若四边形AA1CF的面积为![]() ,则准线l的方程为( )
,则准线l的方程为( )
A.![]() B.
B.![]() C.x=﹣2D.x=﹣1
C.x=﹣2D.x=﹣1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() ,且与坐标轴形成的三角形面积为
,且与坐标轴形成的三角形面积为![]() .求:
.求:
(1)求证:不论![]() 为何实数,直线
为何实数,直线![]() 过定点P;
过定点P;
(2)分别求![]() 和
和![]() 时,所对应的直线条数;
时,所对应的直线条数;
(3)针对![]() 的不同取值,讨论集合
的不同取值,讨论集合![]() 直线
直线![]() 经过P,且与坐标轴围成的三角形面积为
经过P,且与坐标轴围成的三角形面积为![]() 中的元素个数.
中的元素个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的短轴长为
的短轴长为![]() ,离心率为
,离心率为![]() 。
。
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
,![]() 左,右顶点分别为
左,右顶点分别为![]() ,
,![]() ,点
,点![]() ,
,![]() ,为椭圆
,为椭圆![]() 上位于
上位于![]() 轴上方的两点,且
轴上方的两点,且![]() ,记直线
,记直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,若
,若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司推出一新款手机,因其功能强大,外观新潮,一上市便受到消费者争相抢购,销量呈上升趋势.散点图是该款手机上市后前6周的销售数据.
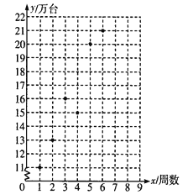
(1)根据散点图,用最小二乘法求![]() 关于
关于![]() 的线性回归方程,并预测该款手机第8周的销量;
的线性回归方程,并预测该款手机第8周的销量;
(2)为了分析市场趋势,该公司市场部从前6周的销售数据中随机抽取2周的数据,记抽取的销量在18万台以上的周数为![]() ,求
,求![]() 的分布列和数学期望.参考公式:回归直线方程
的分布列和数学期望.参考公式:回归直线方程![]() ,其中:
,其中: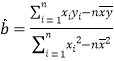 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() )与双曲线
)与双曲线![]() (
(![]() ,
,![]() )有相同的焦点
)有相同的焦点![]() ,点
,点![]() 是两条曲线的一个交点,且
是两条曲线的一个交点,且![]() 轴,则该双曲线经过一、三象限的渐近线的倾斜角所在的区间是( )
轴,则该双曲线经过一、三象限的渐近线的倾斜角所在的区间是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com