
【题目】已知函数 ![]() 的图像与x轴恰有两个公共点,则c= ( )
的图像与x轴恰有两个公共点,则c= ( )
A.-2或2
B.-9或3
C.-1或1
D.-3或1
科目:高中数学 来源: 题型:
【题目】某单位为绿化环境,移栽了甲、乙两种大树各2株.设甲、乙两种大树移栽的成活率分别为![]() 和
和![]() ,且各株大树是否成活互不影响.求移栽的4株大树中:
,且各株大树是否成活互不影响.求移栽的4株大树中:
(1)两种大树各成活1株的概率;
(2)成活的株数![]() 的分布列与期望.
的分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,E、F、G、H分别为AA1、AB、BB1、B1C1的中点,则异面直线EF与GH所成的角等于( ) 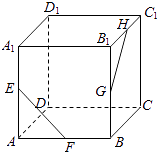
A.45°
B.60°
C.90°
D.120°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com