
【题目】下列说法正确的是( )
A.若a∈R,则“ ![]() <1”是“a>1”的必要不充分条件
<1”是“a>1”的必要不充分条件
B.“p∧q为真命题”是“p∨q为真命题”的必要不充分条件
C.若命题p:“x∈R,sinx+cosx≤ ![]() ”,则¬p是真命题
”,则¬p是真命题
D.命题“x0∈R,使得x02+2x0+3<0”的否定是“x∈R,x2+2x+3>0”
【答案】A
【解析】解:若“ ![]() <1”成立,则“a>1”或“a<0”,故“
<1”成立,则“a>1”或“a<0”,故“ ![]() <1”是“a>1”的不充分条件,
<1”是“a>1”的不充分条件,
若“a>1”成立,则“ ![]() <1”成立,故“
<1”成立,故“ ![]() <1”是“a>1”的必要条件,
<1”是“a>1”的必要条件,
综上所述,“ ![]() <1”是“a>1”的必要不充分条件,故A正确;
<1”是“a>1”的必要不充分条件,故A正确;
若“p∧q为真命题”,则“p,q均为真命题”,则“p∨q为真命题”成立,
若“p∨q为真命题”则“p,q存在至少一个真命题”,则“p∧q为真命题”不一定成立,
综上所述,“p∧q为真命题”是“p∨q为真命题”的充分不必要条件,故B错误;
命题p:“x∈R,sinx+cosx= ![]() sin(x+
sin(x+ ![]() )≤
)≤ ![]() ”为真命题,则¬p是假命题,故C错误;
”为真命题,则¬p是假命题,故C错误;
命题“x0∈R,使得x02+2x0+3<0”的否定是“x∈R,x2+2x+3≥0”,故D错误;
所以答案是:A.
【考点精析】掌握命题的真假判断与应用是解答本题的根本,需要知道两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.


科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,角A,B,C所对的边分别为a,b,c,且3bsinA=c,D为AC边上一点.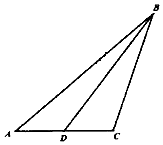
(1)若D是AC的中点,且 ![]() ,
, ![]() ,求△ABC的最短边的边长.
,求△ABC的最短边的边长.
(2)若c=2b=4,S△BCD= ![]() ,求DC的长.
,求DC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产不同规格的一种产品,根据检测标准,其合格产品的质量y(g)与尺寸x(mm)之间近似满足关系式y=axb(a,b为大于0的常数).现随机抽取6件合格产品,测得数据如下:
尺寸(mm) | 38 | 48 | 58 | 68 | 78 | 88 |
质量(g) | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
对数据作了初步处理,相关统计量的值如表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(Ⅰ)根据所给数据,求y关于x的回归方程;
(Ⅱ)按照某项指标测定,当产品质量与尺寸的比在区间( ![]() ,
, ![]() )内时为优等品.现从抽取的6件合格产品中再任选3件,记ξ为取到优等品的件数,试求随机变量ξ的分布列和期望.
)内时为优等品.现从抽取的6件合格产品中再任选3件,记ξ为取到优等品的件数,试求随机变量ξ的分布列和期望.
附:对于一组数据(v1 , u1),(v2 , u2),…,(vn , un),其回归直线u=α+βv的斜率和截距的最小二乘估计分别为 ![]() =
= 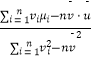 ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司对应聘人员进行能力测试,测试成绩总分为150分.下面是30位应聘人员的测试成绩的测试成绩:64,116,82,93,102,82,104,67,93,118,70,95,119,106,83,72,95,106,72,119,122,95,86,74,131,76,88,108,97,123.
(1)求应聘人员的测试成绩的样本平均数 ![]() (保留小数点后两位);
(保留小数点后两位);
(2)根据以上数据完成下面茎叶图:
应聘人员的测试成绩 | |
6 | |
7 | |
8 | |
9 | |
10 | |
11 | |
12 | |
13 | |
(3)由茎叶图可以认为,应聘人员的测试成绩Z服从正态分布N(μ,σ2),其中μ近似为样本平均数 ![]() ,σ2近似为样本方差s2 , 其中s2=18.872 , 利用该正态分布,求P(76.40<Z<114.14).
,σ2近似为样本方差s2 , 其中s2=18.872 , 利用该正态分布,求P(76.40<Z<114.14).
附:若Z~N(μ,σ2),则P(μ﹣σ<Z<μ+σ)=0.6826,
P(μ﹣2σ<Z<μ+2σ)=0.9544.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学人力资源部计划2016年招聘2名数学教师,共5名应聘者进入最后课堂实录环节.5名数学组评审专家给出评分如表:
评审专家/应聘老师 | 1 | 2 | 3 | 4 | 5 |
评审专家A | 93.0 | 90.0 | 88.5 | 89.5 | 82.5 |
评审专家B | 94.0 | 83.0 | 89.0 | 93.0 | 81.0 |
评审专家C | 91.0 | 85.0 | 81.5 | 88.0 | 81.0 |
评审专家D | 92.0 | 91.5 | 81.0 | 94.5 | 87.0 |
评审专家E | 95.5 | 91.0 | 90.0 | 95.5 | 88.5 |
(Ⅰ)若依据去掉一个最高分和一个最低分规则计算应聘老师成绩,试确定最终应聘成功的2名数学老师的序号;
(Ⅱ)在课堂实录环节,每名应聘老师都需要从5名评审专家中随机选取2名进行点评,且每名应聘老师的选择互不影响,设X表示评审专家A进行点评的次数,求X的分布列以及数学期望;
(Ⅲ)记评审专家A与评审专家B给出的评分的方差分别为 ![]() ,试比较
,试比较 ![]() 与
与 ![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是菱形,∠BAD=60°,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.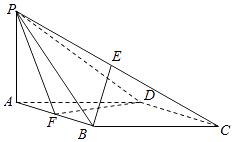
(Ⅰ)求证:BE∥平面PDF;
(Ⅱ)求平面PAB与平面PCD所成的锐二面角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() 的离心率为
的离心率为 ![]() ,F1 , F2分别是它的左、右焦点,且存在直线l,使F1 , F2关于l的对称点恰好为圆C:x2+y2﹣4mx﹣2my+5m2﹣4=0(m∈R,m≠0)的一条直径的两个端点.
,F1 , F2分别是它的左、右焦点,且存在直线l,使F1 , F2关于l的对称点恰好为圆C:x2+y2﹣4mx﹣2my+5m2﹣4=0(m∈R,m≠0)的一条直径的两个端点.
(1)求椭圆E的方程;
(2)设直线l与抛物线y2=2px(p>0)相交于A,B两点,射线F1A,F1B与椭圆E分别相交于点M,N,试探究:是否存在数集D,当且仅当p∈D时,总存在m,使点F1在以线段MN为直径的圆内?若存在,求出数集D;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着网络营销和电子商务的兴起,人们的购物方式更具多样化,某调查机构随机抽取10名购物者进行采访,5名男性购物者中有3名倾向于选择网购,2名倾向于选择实体店,5名女性购物者中有2名倾向于选择网购,3名倾向于选择实体店.
(1)若从10名购物者中随机抽取2名,其中男、女各一名,求至少1名倾向于选择实体店的概率;
(2)若从这10名购物者中随机抽取3名,设X表示抽到倾向于选择网购的男性购物者的人数,求X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com