
【题目】如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,△PCD为等边三角形,平面PAC⊥平面PCD,PA⊥CD,CD=2,AD=3.
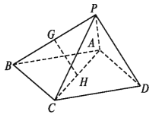
(1)设G,H分别为PB,AC的中点,求证:GH//平面PAD;
(2)求证:![]() ⊥平面PCD;
⊥平面PCD;
(3)求直线AD与平面PAC所成角的正弦值.
 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】某地上年度电价为![]() 元,年用电量为
元,年用电量为![]() 亿千瓦时.本年度计划将电价调至
亿千瓦时.本年度计划将电价调至![]() 之间,经测算,若电价调至
之间,经测算,若电价调至![]() 元,则本年度新增用电量
元,则本年度新增用电量![]() (亿千瓦时)与
(亿千瓦时)与![]() 元成反比例.又当
元成反比例.又当![]() 时,
时,![]() .
.
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)若每千瓦时电的成本价为![]() 元,则电价调至多少时,本年度电力部门的收益将比上年增加
元,则电价调至多少时,本年度电力部门的收益将比上年增加![]() ?[收益=用电量×(实际电价-成本价)]
?[收益=用电量×(实际电价-成本价)]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等比数列a1,a2,a3,a4的公比为q,等差数列b1,b2,b3,b4的公差为d,且![]() .记
.记![]() (i1,2,3,4).
(i1,2,3,4).
(1)求证:数列![]() 不是等差数列;
不是等差数列;
(2)设![]() ,
, ![]() .若数列
.若数列![]() 是等比数列,求b2关于d的函数关系式及其定义域;
是等比数列,求b2关于d的函数关系式及其定义域;
(3)数列![]() 能否为等比数列?并说明理由.
能否为等比数列?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某公司举行的年终庆典活动中,主持人利用随机抽奖软件进行抽奖:由电脑随机生成一张如图所示的3![]() 3表格,其中1格设奖300元,4格各设奖200元,其余4格各设奖100元,点击某一格即显示相应金额.某人在一张表中随机不重复地点击3格,记中奖的总金额为X元.
3表格,其中1格设奖300元,4格各设奖200元,其余4格各设奖100元,点击某一格即显示相应金额.某人在一张表中随机不重复地点击3格,记中奖的总金额为X元.
(1)求概率![]() ;
;
(2)求![]() 的概率分布及数学期望
的概率分布及数学期望![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级参加期末考试的学生中抽出50名学生,并统计了他们的数学成绩(满分为100分),将数学成绩进行分组,并根据各组人数制成如下频率分布表:
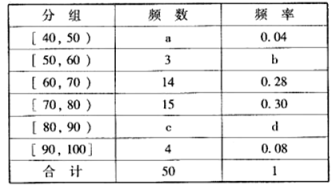
(1)写出![]() 的值,并估计本次考试全年级学生的数学平均分(同一组中的数据用该组区间的中点值作代表);
的值,并估计本次考试全年级学生的数学平均分(同一组中的数据用该组区间的中点值作代表);
(2)现从成绩在![]() 内的学生中任选出两名同学,从成绩在
内的学生中任选出两名同学,从成绩在![]() 内的学生中任选一名同学,共三名同学参加学习习惯问卷调查活动.若
内的学生中任选一名同学,共三名同学参加学习习惯问卷调查活动.若![]() 同学的数学成绩为43分,
同学的数学成绩为43分,![]() 同学的数学成绩为
同学的数学成绩为![]() 分,求
分,求![]() 两同学恰好都被选出的概率.
两同学恰好都被选出的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 是参数),
是参数),
(Ⅰ)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设曲线![]() 经过伸缩变换
经过伸缩变换![]() 得到曲线
得到曲线![]() ,曲线
,曲线![]() 任一点为
任一点为![]() ,求点
,求点![]() 直线
直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com