练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

     我们常用以下方法求形如的函数的导数：先两边同取自然对数得：，再两边同时求导得到：，于是得到：，运用此方法求得函数的一个单调递增区间是

      A.（，4）     B.（3，6）       C（0，）      D.（2，3）

     

    【答案】

     C

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2012•葫芦岛模拟）我们常用以下方法求形如y=f（x）g（x）的函数的导数：先两边同取自然对数得：lny=g（x）lnf（x），再两边同时求导得到：
    1
    y
    •y′=g′（x）lnf（x）+g（x）•
    1
    f(x)
    •f′（x），于是得到：y′=f（x）g（x）[g′（x）lnf（x）+g（x）•
    1
    f(x)
    •f′（x）]，运用此方法求得函数y=x
    1
    x
    的一个单调递增区间是（　　）

    查看答案和解析>>

    科目：高中数学 来源：葫芦岛模拟 题型：单选题

    我们常用以下方法求形如y=f（x）g（x）的函数的导数：先两边同取自然对数得：lny=g（x）lnf（x），再两边同时求导得到：
    1
    y
    •y′=g′（x）lnf（x）+g（x）•
    1
    f(x)
    •f′（x），于是得到：y′=f（x）g（x）[g′（x）lnf（x）+g（x）•
    1
    f(x)
    •f′（x）]，运用此方法求得函数y=x
    1
    x
    的一个单调递增区间是（　　）
    A．（e，4）B．（3，6）C．（0，e）D．（2，3）

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年河北省五校联盟高三（上）调研数学试卷（理科）（解析版） 题型：选择题

    我们常用以下方法求形如y=f（x）g（x）的函数的导数：先两边同取自然对数得：lny=g（x）lnf（x），再两边同时求导得到：•y′=g′（x）lnf（x）+g（x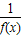）••f′（x），于是得到：y′=f（x）g（x）[g′（x）lnf（x）+g（x）••f′（x）]，运用此方法求得函数y=的一个单调递增区间是（ ）
    A．（e，4）
    B．（3，6）
    C．（0，e）
    D．（2，3）

    查看答案和解析>>

    科目：高中数学 来源：2013年山东省实验中学高考数学二模试卷（理科）（解析版） 题型：选择题

    我们常用以下方法求形如y=f（x）g（x）的函数的导数：先两边同取自然对数得：lny=g（x）lnf（x），再两边同时求导得到：•y′=g′（x）lnf（x）+g（x）••f′（x），于是得到：y′=f（x）g（x）[g′（x）lnf（x）+g（x）••f′（x）]，运用此方法求得函数y=的一个单调递增区间是（ ）
    A．（e，4）
    B．（3，6）
    C．（0，e）
    D．（2，3）

    查看答案和解析>>

    科目：高中数学 来源：2011-2012年辽宁省葫芦岛市高三第三次联考数学试卷（理科）（解析版） 题型：选择题

    我们常用以下方法求形如y=f（x）g（x）的函数的导数：先两边同取自然对数得：lny=g（x）lnf（x），再两边同时求导得到：•y′=g′（x）lnf（x）+g（x）••f′（x），于是得到：y′=f（x）g（x）[g′（x）lnf（x）+g（x）••f′（x）]，运用此方法求得函数y=的一个单调递增区间是（ ）
    A．（e，4）
    B．（3，6）
    C．（0，e）
    D．（2，3）

    查看答案和解析>>

    同步练习册答案