
| A. | (1,$\sqrt{6}$) | B. | (2,$\sqrt{7}$) | C. | (2,$\sqrt{6}$) | D. | (1,$\sqrt{7}$) |
分析 先确定M的轨迹是直线x=2,代入椭圆方程,得y2=6,即可得出结论.
解答 解:设A(x1,y1),B(x2,y2),M(x0,y0),
代入椭圆方程相减,整理得(y1+y2)(y1-y2)=4(x1-x2),
当l的斜率存在时,利用点差法可得2ky0=-x0,
因为直线与圆相切,所以$\frac{{y}_{0}}{{x}_{0}-1}$=-$\frac{1}{k}$,所以x0=2,
即M的轨迹是直线x=2.
将x=2代入椭圆方程,得y2=6,
∴-$\sqrt{6}$<y0<$\sqrt{6}$,
∵M在圆上,
∴(x0-1)2+y02=r2,
∴r2=y02+1≤7,
∵直线l恰有4条,
∴y0≠0,
∴1<r2<7,
故1<r<$\sqrt{7}$时,直线l有2条;
斜率不存在时,直线l有2条;
所以直线l恰有4条,1<r<$\sqrt{7}$,
故选D.
点评 本题考查直线与椭圆、圆的位置关系,考查点差法,考查学生分析解决问题的能力,属于中档题.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{1}{32}$ | B. | x=$\frac{1}{2}$ | C. | y=2 | D. | y=4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
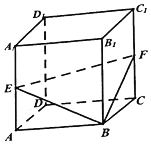 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E,F分别是棱AA1,CC1的中点,P是侧面BCC1B1内一点,若A1P∥平面BEF,则线段A1P长度的取值范围是[$\frac{\sqrt{30}}{5}$,$\sqrt{2}$].
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E,F分别是棱AA1,CC1的中点,P是侧面BCC1B1内一点,若A1P∥平面BEF,则线段A1P长度的取值范围是[$\frac{\sqrt{30}}{5}$,$\sqrt{2}$].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | $\frac{4}{3}$ | C. | -$\frac{1}{7}$ | D. | -$\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | ||
| C. | 2个 | D. | 不确定,随k的变化而变化 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com