
【题目】已知函数![]() .
.
![]() 若函数
若函数![]() ,求
,求![]() 在
在![]() 上的最小值;
上的最小值;
![]() Ⅱ
Ⅱ![]() 记函数
记函数![]() ,若函数
,若函数![]() 在
在![]() 上有两个零点
上有两个零点![]() ,
,![]() ,求实数a的取值范围,并证明
,求实数a的取值范围,并证明![]() .
.
【答案】(Ⅰ)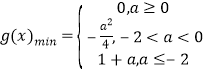 ;(Ⅱ)见证明
;(Ⅱ)见证明
【解析】
![]() Ⅰ
Ⅰ![]() 求得
求得![]() 的对称轴,讨论当
的对称轴,讨论当![]() ,当
,当![]() ,当
,当![]() ,结合偶函数的性质和单调性,可得所求最小值;
,结合偶函数的性质和单调性,可得所求最小值;
![]() Ⅱ
Ⅱ![]() 令
令![]() ,
,![]() ,函数
,函数![]() 在
在![]() 上有两个零点
上有两个零点![]() ,
,![]() 等价于
等价于![]() 在
在![]() 上有两个零点
上有两个零点![]() ,
,![]() ,分类讨论,结合
,分类讨论,结合![]() 的单调性和韦达定理,可得所求a的范围;运用分析法证明
的单调性和韦达定理,可得所求a的范围;运用分析法证明![]() 即证
即证![]() ,运用
,运用![]() 的解析式即可得证.
的解析式即可得证.
![]() Ⅰ
Ⅰ![]() 函数
函数![]() 的对称轴为
的对称轴为![]() ,
,
![]() 当
当![]() ,即
,即![]() 时,
时,
![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
所以![]() ;
;
![]() 当
当![]() ,即
,即![]() 时,
时,
![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,在
上递增,在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
所以![]() ;
;
![]() 当
当![]() ,即
,即![]() 时,
时,
![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,
上递减,
所以![]() .
.
综上所述,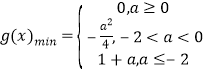 ;
;
![]() Ⅱ
Ⅱ![]() 令
令![]() ,
,![]() ,
,
函数![]() 在
在![]() 上有两个零点
上有两个零点![]() ,
,![]() 等价于
等价于
![]() 在
在![]() 上有两个零点
上有两个零点![]() ,
,![]() ,
,
不妨设![]() ,
,
因为![]() ,
,
所以![]() 在
在![]() 上是单调函数,
上是单调函数,
所以![]() 在
在![]() 上至多只有一个解,
上至多只有一个解,
当![]() 时,
时,![]() ,不符合题意;
,不符合题意;
当![]() 时,由
时,由![]() 得
得![]() ;
;
由![]() ,得
,得![]() ,
,
综上,当![]() 时,函数
时,函数![]() 在
在![]() 上有两个零点
上有两个零点![]() ,
,![]() .
.
要证![]() ,即证
,即证![]() ,
,
当![]() 时,
时,![]() ,得
,得![]() ,
,
因为![]() ,所以
,所以![]() ,
,
即![]() .
.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:
【题目】若函数![]() 在定义域内存在实数
在定义域内存在实数![]() ,使得
,使得![]() 成立,则称函数
成立,则称函数![]() 有“飘移点”
有“飘移点”![]() .
.
![]() Ⅰ
Ⅰ![]() 试判断函数
试判断函数![]() 及函数
及函数![]() 是否有“飘移点”并说明理由;
是否有“飘移点”并说明理由;
![]() Ⅱ
Ⅱ![]() 若函数
若函数![]() 有“飘移点”,求a的取值范围.
有“飘移点”,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年8月8日是我国第十个全民健身日,其主题是:新时代全民健身动起来。某市为了解全民健身情况,随机从某小区居民中抽取了40人,将他们的年龄分成7段:[10,20),[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图所示的频率分布直方图。

(1)试求这40人年龄的平均数、中位数的估计值;
(2)(i)若从样本中年龄在[50,70)的居民中任取2人赠送健身卡,求这2人中至少有1人年龄不低于60岁的概率;
(ⅱ)已知该小区年龄在[10,80]内的总人数为2000,若18岁以上(含18岁)为成年人,试估计该小区年龄不超过80岁的成年人人数。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题的说法错误的是( )
A.若“p∨q”为假命题,则p,q均为假命题
B.“x=1”是“x≥1”的充分不必要条件
C.“sinx=![]() ”的必要不充分条件是“x=
”的必要不充分条件是“x=![]() ”
”
D.若命题p:?x0∈R,x02≥0,则命题¬p:?x∈R,x2<0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)满足f(﹣x)=f(x),且f(x+2)=f(x)+f(2),当x∈[0,1]时,f(x)=x,那么在区间[﹣1,3]内,关于x的方程f(x)=kx+k+1(k∈R)且k≠﹣1恰有4个不同的根,则k的取值范围是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为缓减人口老年化带来的问题,中国政府在2016年1月1日作出全国统一实施全面的“二孩”政策,生“二孩”是目前中国比较流行的元素。某调查机构对某校学生做了一个是否同意父母生“二孩”抽样调查,该调查机构从该校随机抽查了100名不同性别的学生,调查统计他们是同意父母生“二孩”还是反对父母生“二孩”.现已得知100人中同意父母生“二孩”占75%,统计情况如下表:

(1)请补充完整上述列联表;
(2)根据以上资料你是否有95%把握,认为是否同意父母生“二孩”与性别有关?请说明理由.
参考公式与数据:![]() ,其中
,其中![]()

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com