
ΓΨΧβΡΩΓΩ2019Ρξ÷ΘΩΣΙζΦ ¬μά≠Υ…±»»ϋΘ§”Ύ2019Ρξ3‘¬31»’‘Ύ÷Θ÷ίΓΔΩΣΖβΨΌ––Θ°Ρ≥―ß–Θ±ΨΉ≈ΓΑΈ“‘ΥΕ·Θ§Έ“Ωλά÷Θ§Έ“ΕΆΝΕΘ§Έ“ΧαΗΏΓ±ΨΪ…ώΘ§ΜΐΦΪΉι÷·―ß…ζ≤ΈΦ”±»»ϋΦΑœύΙΊΜνΕ·Θ§ΈΣΝΥΝΥΫβ―ß…ζΒΡ≤Έ”κ«ιΩωΘ§¥”»Ϊ–Θ―ß…ζ÷–ΥφΜζ≥ι»ΓΝΥ150Οϊ―ß…ζΘ§Ε‘ «Ζώ≤Έ”κΒΡ«ιΩωΫχ––ΝΥΈ ΨμΒς≤ιΘ§Ά≥ΦΤ ΐΨί»γœ¬ΘΚ
Μα≤Έ”κ | ≤ΜΜα≤Έ”κ | |
Ρ–…ζ | 60 | 40 |
≈°…ζ | 20 | 30 |
Θ®1Θ©ΗυΨί…œ±μΥΒΟςΘ§ΡήΖώ”–97.5%ΒΡΑ―Έ’»œΈΣ≤Έ”κ¬μά≠Υ…»ϋ ¬”κ–‘±π”–ΙΊ?
Θ®2Θ©œ÷¥”≤Έ”κΈ ΨμΒς≤ι«“≤Έ”κ»ϋ ¬ΒΡ―ß…ζ÷–Θ§≤…”ΟΑ¥–‘±πΖ÷≤ψ≥ι―υΒΡΖΫΖ®―Γ»Γ8»Υ≤ΈΦ”2019Ρξ¬μά≠Υ…±»»ϋ÷Ψ‘Η’Ώ–ϊ¥ΪΜνΕ·Θ§
ΔΌ«σΡ–ΓΔ≈°―ß…ζΗς―Γ»ΓΕύ…Ό»ΥΘΜ
ΔΎ»τ¥”’β8»Υ÷–ΥφΜζ―Γ»Γ2»ΥΒΫ–ΘΙψ≤Ξ’ΨΩΣ’Ι2019Ρξ»ϋ ¬–ϊ¥ΪΫι…ήΘ§«σ«ΓΚΟ―ΓΒΫ2ΟϊΡ–…ζΒΡΗ≈¬ Θ°
ΗΫΘΚ≤ΈΩΦΙΪ ΫΘΚ![]() Θ§Τδ÷–
Θ§Τδ÷–![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
ΓΨ¥πΑΗΓΩΘ®1Θ©”–97.5ΘΞΒΡΑ―Έ’»œΈΣ≤Έ”κ¬μά≠Υ…»ϋ ¬”κ–‘±π”–ΙΊΘΜΘ®2Θ©ΔΌΡ–…ζ―Γ![]() »ΥΘ§≈°…ζ―Γ
»ΥΘ§≈°…ζ―Γ![]() »ΥΘΜΔΎ
»ΥΘΜΔΎ![]() .
.
ΓΨΫβΈωΓΩ
Θ®1Θ©άϊ”Ο![]() ΦΤΥψΫαΙϊΘ§Ά®Ιΐ±»ΫœΦ¥Ω…≈–ΕœΡήΖώ”–97.5%ΒΡΑ―Έ’»œΈΣ≤Έ”κ¬μά≠Υ…»ϋ ¬”κ–‘±π”–ΙΊΘΜ
ΦΤΥψΫαΙϊΘ§Ά®Ιΐ±»ΫœΦ¥Ω…≈–ΕœΡήΖώ”–97.5%ΒΡΑ―Έ’»œΈΣ≤Έ”κ¬μά≠Υ…»ϋ ¬”κ–‘±π”–ΙΊΘΜ
Θ®2Θ©ΔΌΗυΨίΖ÷≤ψ≥ι―υΖΫΖ®Ω…ΒΟΘ§―Γ»ΓΒΡ8»Υ÷–Θ§Ρ–…ζΚΆ≈°…ζ»Υ ΐΘΜΔΎΆ®ΙΐΝ–ΨΌΘ§Ω…ΒΟ≥ω8»Υ÷–―Γ»ΓΝΫ»ΥΙ≤”–28÷÷«ιΩωΘ§Εχ―ΓΒΫ2Ρ–ΒΡΙ≤15÷÷«ιΩωΘ§άϊ”ΟΙ≈ΒδΗ≈–ΆΗ≈¬ ΒΡ«σΖ®Φ¥Ω…«σ≥ωΫαΙϊ.
Θ®1Θ©“ρΈΣ![]() Θ§
Θ§
Υυ“‘”–97.5ΘΞΒΡΑ―Έ’»œΈΣ≤Έ”κ¬μά≠Υ…»ϋ ¬”κ–‘±π”–ΙΊΘ°
Θ®2Θ©ΔΌΗυΨίΖ÷≤ψ≥ι―υΖΫΖ®ΒΟΘ§Ρ–…ζ![]() »ΥΘ§≈°…ζ2»ΥΘ§
»ΥΘ§≈°…ζ2»ΥΘ§
Υυ“‘―Γ»ΓΒΡ8»Υ÷–Θ§Ρ–…ζ”–6»ΥΘ§≈°…ζ”–2»ΥΘ°
ΔΎ…η≥ι»ΓΒΡ![]() ΟϊΡ–…ζΖ÷±πΈΣ
ΟϊΡ–…ζΖ÷±πΈΣ![]() Θ§2Οϊ≈°…ζΈΣ
Θ§2Οϊ≈°…ζΈΣ![]() ΘΜ
ΘΜ
¥”÷–≥ι»ΓΝΫ»ΥΘ§Ζ÷±πΦ«ΈΣ![]() Θ§
Θ§![]() ,
,![]() ,
,![]() Θ§
Θ§
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() Ι≤28÷÷«ιΩωΘ§
Ι≤28÷÷«ιΩωΘ§
Τδ÷–≥ι»ΓΒΫ2ΟϊΡ–…ζΒΡΙ≤15÷÷«ιΩωΘ§
Υυ“‘Θ§«ΓΚΟ―ΓΒΫ2ΟϊΡ–…ζΒΡΗ≈¬ ![]() Θ°
Θ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ‘ΎΦΪΉχœΒ÷–Θ§Βψ![]() »ΤΦΪΒψ
»ΤΦΪΒψ![]() Υ≥ ±’κ–ΐΉΣΫ«
Υ≥ ±’κ–ΐΉΣΫ«![]() ΒΟΒΫΒψ
ΒΟΒΫΒψ![]() .“‘
.“‘![]() ΈΣ‘≠ΒψΘ§ΦΪ÷αΈΣ
ΈΣ‘≠ΒψΘ§ΦΪ÷αΈΣ![]() ÷αΖ«ΗΚΑκ÷αΘ§≤Δ»ΓœύΆ§ΒΡΒΞΈΜ≥ΛΕ»Ϋ®ΝΔΤΫΟφ÷±Ϋ«Ήχ±ξœΒΘ§«ζœΏ
÷αΖ«ΗΚΑκ÷αΘ§≤Δ»ΓœύΆ§ΒΡΒΞΈΜ≥ΛΕ»Ϋ®ΝΔΤΫΟφ÷±Ϋ«Ήχ±ξœΒΘ§«ζœΏ![]() »Τ
»Τ![]() Ρφ ±’κ–ΐΉΣ
Ρφ ±’κ–ΐΉΣ![]() ΒΟΒΫ«ζœΏ
ΒΟΒΫ«ζœΏ![]() .
.
Θ®1Θ©«σ«ζœΏ![]() ΒΡ÷±Ϋ«Ήχ±ξΖΫ≥ΧΘΜ
ΒΡ÷±Ϋ«Ήχ±ξΖΫ≥ΧΘΜ
Θ®2Θ©Βψ![]() ΒΡΦΪΉχ±ξΈΣ
ΒΡΦΪΉχ±ξΈΣ![]() Θ§÷±œΏ
Θ§÷±œΏ![]() ΙΐΒψ
ΙΐΒψ![]() «“”κ«ζœΏ
«“”κ«ζœΏ![]() ΫΜ”Ύ
ΫΜ”Ύ![]() ΝΫΒψΘ§«σ
ΝΫΒψΘ§«σ![]() ΒΡΉν–Γ÷Β.
ΒΡΉν–Γ÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΆ÷‘≤![]() Θ®
Θ®![]() ΈΣ≥Θ ΐ«“
ΈΣ≥Θ ΐ«“![]() Θ©”κ÷±œΏ
Θ©”κ÷±œΏ![]() ”–«“÷Μ”–“ΜΗωΙΪΙ≤Βψ
”–«“÷Μ”–“ΜΗωΙΪΙ≤Βψ![]() Θ§
Θ§![]() Θ°
Θ°
Θ®ΔώΘ©Β±Βψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() ±Θ§«σ÷±œΏ
±Θ§«σ÷±œΏ![]() ΒΡΖΫ≥ΧΘΜ
ΒΡΖΫ≥ΧΘΜ
Θ®ΔρΘ©ΙΐΆ÷‘≤![]() ΒΡΝΫΫΙΒψ
ΒΡΝΫΫΙΒψ![]() Θ§
Θ§![]() Ής÷±œΏ
Ής÷±œΏ![]() ΒΡ¥ΙœΏΘ§¥ΙΉψΖ÷±πΈΣ
ΒΡ¥ΙœΏΘ§¥ΙΉψΖ÷±πΈΣ![]() Θ§
Θ§![]() Θ§«σΥΡ±Ώ–Έ
Θ§«σΥΡ±Ώ–Έ![]() ΟφΜΐΒΡΉν¥σ÷ΒΘ®”Ο
ΟφΜΐΒΡΉν¥σ÷ΒΘ®”Ο![]() ±μ ΨΘ©Θ°
±μ ΨΘ©Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ![]() ΡΎΘ§“―÷Σ
ΡΎΘ§“―÷Σ![]() Θ§Ιΐ÷±œΏ
Θ§Ιΐ÷±œΏ![]() Θ§
Θ§![]() Ζ÷±πΉςΤΫΟφ
Ζ÷±πΉςΤΫΟφ![]() Θ§
Θ§![]() Θ§ Ι»ώΕΰΟφΫ«
Θ§ Ι»ώΕΰΟφΫ«![]() ΈΣ
ΈΣ![]() Θ§»ώΕΰΟφΫ«
Θ§»ώΕΰΟφΫ«![]() ΈΣ
ΈΣ![]() Θ§‘ρΤΫΟφ
Θ§‘ρΤΫΟφ![]() ”κΤΫΟφ
”κΤΫΟφ![]() Υυ≥…ΒΡ»ώΕΰΟφΫ«ΒΡ”ύœ“÷ΒΈΣΘ® Θ©.
Υυ≥…ΒΡ»ώΕΰΟφΫ«ΒΡ”ύœ“÷ΒΈΣΘ® Θ©.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥ΗωΈΔ–≈»ΚΡ≥¥ΈΫχ––ΒΡ«άΚλΑϋΜνΕ·÷–Θ§»Κ÷ςΥυΖΔΚλΑϋΒΡΉήΫπΕνΈΣ10‘ΣΘ§±ΜΥφΜζΖ÷≈δΈΣ2.49‘ΣΓΔ1.32‘ΣΓΔ2.19‘ΣΓΔ0.63‘ΣΓΔ3.37‘ΣΙ≤5ΖίΘ§Ι©ΦΉΓΔ““Β»5»Υ«άΘ§ΟΩ»Υ÷ΜΡή«ά“Μ¥ΈΘ§‘ρΦΉΓΔ““Εΰ»Υ«άΒΫΒΡΫπΕν÷°ΚΆ≤ΜΒΆ”Ύ4‘ΣΒΡΗ≈¬ «Θ® Θ©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈ“Ιζ’ΰΗ°Ε‘PM2.5≤…”Ο»γœ¬±ξΉΦΘΚ

Ρ≥ –ΜΖ±ΘΨ÷¥”180ΧλΒΡ –«χPM2.5Φύ≤β ΐΨί÷–Θ§ΥφΜζ≥ι»Γ10ΧλΒΡ ΐΨίΉςΈΣ―υ±ΨΘ§Φύ≤β÷Β»γΨΞ“ΕΆΦΥυ ΨΘ® °ΈΜΈΣΨΞΘ§ΗωΈΜΈΣ“ΕΘ©.
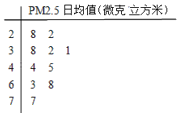
Θ®1Θ©«σ’β10Χλ ΐΨίΒΡ÷–ΈΜ ΐ.
Θ®2Θ©¥”’β10ΧλΒΡ ΐΨί÷–»Έ»Γ3ΧλΒΡ ΐΨίΘ§Φ«![]() ±μ ΨΩ’Τχ÷ ΝΩ¥οΒΫ“ΜΦΕΒΡΧλ ΐΘ§«σ
±μ ΨΩ’Τχ÷ ΝΩ¥οΒΫ“ΜΦΕΒΡΧλ ΐΘ§«σ![]() ΒΡΖ÷≤ΦΝ–ΘΜ
ΒΡΖ÷≤ΦΝ–ΘΜ
Θ®3Θ©“‘’β10ΧλΒΡPM2.5»’Ψυ÷Βά¥ΙάΦΤ’β180ΧλΒΡΩ’Τχ÷ ΝΩ«ιΩωΘ§Φ«![]() ΈΣ’β180ΧλΩ’Τχ÷ ΝΩ¥οΒΫ“ΜΦΕΒΡΧλ ΐΘ§«σ
ΈΣ’β180ΧλΩ’Τχ÷ ΝΩ¥οΒΫ“ΜΦΕΒΡΧλ ΐΘ§«σ![]() ΒΡΨυ÷Β.
ΒΡΨυ÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ ΐΝ–{an}¬ζΉψΘ§an+1ΘΫan+1![]() Θ§a1ΘΫaΘ§‘ρ“ΜΕ®¥φ‘ΎaΘ§ Ι ΐΝ–÷–Θ® Θ©
Θ§a1ΘΫaΘ§‘ρ“ΜΕ®¥φ‘ΎaΘ§ Ι ΐΝ–÷–Θ® Θ©
A.¥φ‘ΎnΓ N*Θ§”–an+1an+2ΘΦ0
B.¥φ‘ΎnΓ N*Θ§”–Θ®an+1©¹1Θ©Θ®an+2©¹1Θ©ΘΦ0
C.¥φ‘ΎnΓ N*Θ§”–![]()
D.¥φ‘ΎnΓ N*Θ§”–![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§’ΐΖΫΧεABCDΘ≠EFGHΒΡ“ΜΗωΫΊΟφΨ≠ΙΐΕΞΒψAΓΔCΦΑάβEF…œ“ΜΒψKΘ§«“ΫΪ’ΐΖΫΧεΖ÷≥…ΧεΜΐ±»ΈΣ3ΘΚ1ΒΡΝΫ≤ΩΖ÷Θ§‘ρ![]() ΒΡ÷ΒΈΣ______ .
ΒΡ÷ΒΈΣ______ .
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΆ÷‘≤![]() ΒΡάκ–Ρ¬ ΈΣ
ΒΡάκ–Ρ¬ ΈΣ![]() «
«![]() …œ“ΜΒψΘ°
…œ“ΜΒψΘ°
Θ®1Θ©«σΆ÷‘≤![]() ΒΡΖΫ≥ΧΘΜ
ΒΡΖΫ≥ΧΘΜ
Θ®2Θ©…η![]() «
«![]() Ζ÷±πΙΊ”ΎΝΫΉχ±ξ÷αΦΑΉχ±ξ‘≠ΒψΒΡΕ‘≥ΤΒψΘ§ΤΫ––”Ύ
Ζ÷±πΙΊ”ΎΝΫΉχ±ξ÷αΦΑΉχ±ξ‘≠ΒψΒΡΕ‘≥ΤΒψΘ§ΤΫ––”Ύ![]() ΒΡ÷±œΏ
ΒΡ÷±œΏ![]() ΫΜ
ΫΜ![]() ”Ύ“λ”Ύ
”Ύ“λ”Ύ![]() ΒΡΝΫΒψ
ΒΡΝΫΒψ![]() Θ°Βψ
Θ°Βψ![]() ΙΊ”Ύ‘≠ΒψΒΡΕ‘≥ΤΒψΈΣ
ΙΊ”Ύ‘≠ΒψΒΡΕ‘≥ΤΒψΈΣ![]() Θ°÷ΛΟςΘΚ÷±œΏ
Θ°÷ΛΟςΘΚ÷±œΏ![]() ”κ
”κ![]() ÷αΈß≥…ΒΡ»ΐΫ«–Έ «Β»―ϋ»ΐΫ«–ΈΘ°
÷αΈß≥…ΒΡ»ΐΫ«–Έ «Β»―ϋ»ΐΫ«–ΈΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com