
【题目】在平面直角坐标系xOy中,已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,定点A(-2,0),B(2,0).
,定点A(-2,0),B(2,0).

(1) 若椭圆C上存在点T,使得![]() ,求椭圆C的离心率的取值范围;
,求椭圆C的离心率的取值范围;
(2) 已知点![]() 在椭圆C上.
在椭圆C上.
①求椭圆C的方程;
②记M为椭圆C上的动点,直线AM,BM分别与椭圆C交于另一点P,Q,若![]() ,
, ![]() .求λ+μ的值.
.求λ+μ的值.
【答案】(1)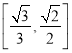 ;(2)①
;(2)①![]() ;②6
;②6
【解析】试题分析:(1)先求出动点![]() 的轨迹方程,设出椭圆方程,与
的轨迹方程,设出椭圆方程,与![]() 的轨迹方程联立求出
的轨迹方程联立求出![]() ,根据椭圆横坐标的有界性求出
,根据椭圆横坐标的有界性求出![]() 的范围,离心率表示为
的范围,离心率表示为![]() 的函数,求出函数的值域即可得结果;(2)①根据点
的函数,求出函数的值域即可得结果;(2)①根据点![]() 在椭圆C上,结合(1)的结论可得椭圆方程,②设出点
在椭圆C上,结合(1)的结论可得椭圆方程,②设出点![]() ,根据
,根据![]() ,
, ![]() 分别求出
分别求出![]() 用
用![]() 表示, 列方程化简即可得结果.
表示, 列方程化简即可得结果.
试题解析:(1)设点T(x,y),由![]() =
=![]() ,得(x+2)2+y2=2[(x+1)2+y2],即x2+y2=2.
,得(x+2)2+y2=2[(x+1)2+y2],即x2+y2=2.
由 得y2=m2-m,(其中:m=
得y2=m2-m,(其中:m=![]() )
)
因此0≤m2-m≤m,解得1≤m≤2,所以椭圆的离心率e=![]() ∈
∈![]() .
.
(2) ①椭圆C的方程为![]() .
.
②设M(x0,y0),P(x1,y1),Q(x2,y2),![]()
![]() 得
得![]() 从而
从而![]()
因为![]() +y=1,所以
+y=1,所以![]() +(λy1)2=1,
+(λy1)2=1,
即λ2![]() +2λ(λ-1)x1+2(λ-1)2-1=0.
+2λ(λ-1)x1+2(λ-1)2-1=0.
因为![]() +y=1,代入得2λ(λ-1)x1+3λ2-4λ+1=0.
+y=1,代入得2λ(λ-1)x1+3λ2-4λ+1=0.
由题意知,λ≠1,故x1=-![]() ,所以x0=
,所以x0=![]() ,同理可得x0=
,同理可得x0=![]() .
.
因此![]() =
=![]() ,所以λ+μ=6为定值.
,所以λ+μ=6为定值.


科目:高中数学 来源: 题型:
【题目】给定一个数列{an},在这个数列里,任取m(m≥3,m∈N*)项,并且不改变它们在数列{an}中的先后次序,得到的数列称为数列{an}的一个m阶子数列.已知数列{an}的通项公式为an=![]() (n∈N*,a为常数),等差数列a2,a3,a6是数列{an}的一个3阶子数列.
(n∈N*,a为常数),等差数列a2,a3,a6是数列{an}的一个3阶子数列.
(1)求a的值;
(2)等差数列b1,b2,…,bm是{an}的一个m (m≥3,m∈N*) 阶子数列,且b1=![]() (k为常数,k∈N*,k≥2),求证:m≤k+1;
(k为常数,k∈N*,k≥2),求证:m≤k+1;
(3)等比数列c1,c2,…,cm是{an}的一个m (m≥3,m∈N*) 阶子数列,
求证:c1+c2+…+cm≤2-![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)已知动圆![]() 过定点
过定点![]() 且与
且与![]() 轴截得的弦
轴截得的弦![]() 的长为
的长为![]() .
.
(Ⅰ)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)已知点![]() ,动直线
,动直线![]() 和坐标轴不垂直,且与轨迹
和坐标轴不垂直,且与轨迹![]() 相交于
相交于![]() 两点,试问:在
两点,试问:在![]() 轴上是否存在一定点
轴上是否存在一定点![]() ,使直线
,使直线![]() 过点
过点![]() ,且使得直线
,且使得直线![]() ,
,![]() ,
,![]() 的斜率依次成等差数列?若存在,请求出定点
的斜率依次成等差数列?若存在,请求出定点![]() 的坐标;否则,请说明理由.
的坐标;否则,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“抛阶砖”是国外游乐场的典型游戏之一.参与者只需将手上的“金币”(设“金币”的半径为1)抛向离身边若干距离的阶砖平面上,抛出的“金币”若恰好落在任何一个阶砖(边长为2.1的正方形)的范围内(不与阶砖相连的线重叠),便可获大奖.不少人被高额奖金所吸引,纷纷参与此游戏,但很少有人得到奖品,请用所学的概率知识解释这是为什么.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com