
 米,钢筋网的总长度为
米,钢筋网的总长度为 米.
米.
 与
与 的函数关系式,并写出其定义域;
的函数关系式,并写出其定义域;
 米
米 


 不扣分
不扣分


 即
即 时取等号,此时宽为:
时取等号,此时宽为: 米
米

 ,
,
 当
当 时,
时,

 在
在 上是单调递减函数
上是单调递减函数 当
当 时,
时, ,此时,长为25米,宽为
,此时,长为25米,宽为 米
米 ,
, ,
,
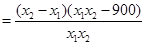
 ,
,
 ,
, 
 在
在 上是单调递减函数
上是单调递减函数  当
当 时,
时,
 米
米

科目:高中数学 来源:不详 题型:单选题
 ,则f(x)≥﹣2的解集是( )
,则f(x)≥﹣2的解集是( )A.(﹣∞,﹣ ]∪[4,+∞) ]∪[4,+∞) | B.(﹣∞,﹣ ]∪(0,4] ]∪(0,4] |
C.(﹣ ,0]∪[4,+∞) ,0]∪[4,+∞) | D.(﹣ ,0]∪(0,4] ,0]∪(0,4] |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,若存在区间
,若存在区间 ,使得
,使得 ,则称函数
,则称函数 为“可等域函数”,区间
为“可等域函数”,区间 为函数
为函数 的一个“可等域区间”. 下列函数中存在唯一“可等域区间”的“可等域函数”为( )
的一个“可等域区间”. 下列函数中存在唯一“可等域区间”的“可等域函数”为( )A. | B. |
C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
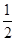 t+30(1≤t≤30,t∈N),后20天价格为g(t)=45(31≤t≤50,t∈N).
t+30(1≤t≤30,t∈N),后20天价格为g(t)=45(31≤t≤50,t∈N).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com