
【题目】某校拟从甲、乙两名同学中选一人参加疫情知识问答竞赛,于是抽取了甲、乙两人最近同时参加校内竞赛的十次成绩,将统计情况绘制成如图所示的折线图.根据该折线图,下面结论正确的是( )
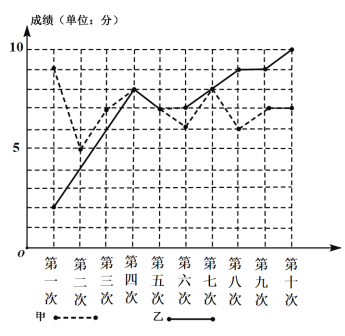
A.甲、乙成绩的中位数均为7
B.乙的成绩的平均分为6.8
C.甲从第四次到第六次成绩的下降速率要大于乙从第四次到第五次的下降速率
D.甲的成绩的方差小于乙的成绩的方差
【答案】D
【解析】
在A中,将乙十次的成绩从小到大排列,求出中位数为7.5;在B中,求出乙的成绩的平均分为7;在C中,从折线图可以看出甲第6次所对应的点与乙第4次和第5次所对应的点均在同一条直线上,故下降速率相同;在D中,从折线图可以看出,乙的成绩比甲的成绩波动更大,甲的成绩的方差小于乙的成绩的方差.
在A中,将乙十次的成绩从小到大排列,
为2,4,6,7,7,8,8,9,9,10,
∴中位数为![]() ,故A错误;
,故A错误;
在B中,乙的成绩的平均分为:![]() (2+4+6+7+7+8+8+9+9+10)=7,故B错误;
(2+4+6+7+7+8+8+9+9+10)=7,故B错误;
在C中,从折线图可以看出甲第6次所对应的点与乙第4次和第5次所对应的点均在同一条直线上,
故下降速率相同,故C错误;
在D中,从折线图可以看出,乙的成绩比甲的成绩波动更大,
∴甲的成绩的方差小于乙的成绩的方差,故D正确.
故选:D.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
【题目】下图统计了截止到2019年年底中国电动汽车充电桩细分产品占比及保有量情况,关于这5次统计,下列说法正确的是( )
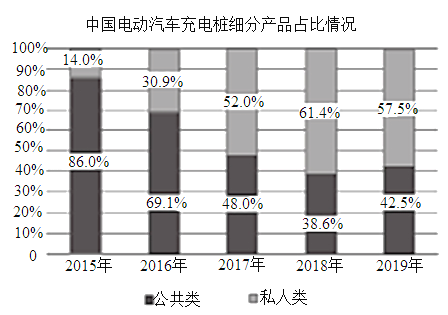
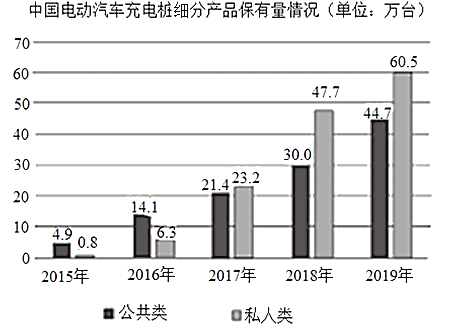
A.私人类电动汽车充电桩保有量增长率最高的年份是2018年
B.公共类电动汽车充电桩保有量的中位数是25.7万台
C.公共类电动汽车充电桩保有量的平均数为23.12万台
D.从2017年开始,我国私人类电动汽车充电桩占比均超过50%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点为极点,![]() 轴非负半轴为极轴,长度单位相同,建立极坐标系,曲线
轴非负半轴为极轴,长度单位相同,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 过点
过点![]() 倾斜角为
倾斜角为![]() .
.
(1)将曲线![]() 的极坐标方程化为直角坐标方程,并写出直线
的极坐标方程化为直角坐标方程,并写出直线![]() 的参数方程;
的参数方程;
(2)当![]() 时,直线
时,直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,M为
,M为![]() 上的一点,以
上的一点,以![]() 为折痕把
为折痕把![]() 折起,使点D到达点P的位置,且平面
折起,使点D到达点P的位置,且平面![]() 平面
平面![]() .连接
.连接![]() ,
,![]() ,点N为
,点N为![]() 的中点,且
的中点,且![]() 平面
平面![]() .
.
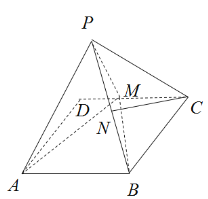
(1)求线段![]() 的长;
的长;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,直线
,直线![]() :
:![]() ,点
,点![]() 为
为![]() 上一动点,过
上一动点,过![]() 作直线
作直线![]() ,
,![]() 为
为![]() 的中垂线,
的中垂线,![]() 与
与![]() 交于点
交于点![]() ,设点
,设点![]() 的轨迹为曲线Γ.
的轨迹为曲线Γ.
(1)求曲线Γ的方程;
(2)若过![]() 的直线与Γ交于
的直线与Γ交于![]() 两点,线段
两点,线段![]() 的垂直平分线交
的垂直平分线交![]() 轴于点
轴于点![]() ,求
,求![]() 与
与![]() 的比值.
的比值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com