
分析 求此双曲线的渐近线方程即求$\frac{b}{a}$的值,这和求双曲线离心率是一样的思路,只要在直角三角形PF2F1中由双曲线定义找到a、b、c间的等式,再利用c2=a2+b2即可得$\frac{b}{a}$的值
解答 解:在Rt△PF2F1中,设|PF1|=d1,|PF2|=d2,∵∠PF1F2=30°
∴$\left\{\begin{array}{l}{{d}_{1}=2{d}_{2}}\\{{d}_{1}-{d}_{2}=2a}\end{array}\right.$∴d2=2a
∵|F2F1|=2c
∴tan30°=$\frac{2a}{2c}$
∴$\frac{a}{c}$=$\frac{\sqrt{3}}{3}$,即$\frac{{a}^{2}}{{a}^{2}+{b}^{2}}$=$\frac{1}{3}$
∴($\frac{a}{b}$)2=2
∴$\frac{a}{b}$=$\sqrt{2}$
∴双曲线的渐近线方程为y=±$\sqrt{2}$x
点评 本题考查了双曲线的定义及其几何性质,求双曲线渐近线方程的思路和方法,恰当利用几何条件是解决本题的关键


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
 如图,ABCD-A1B1C1D1是正方体,O、M、N分别是B1D1、AB1、AD1的中点,直线A1C交平面AB1D1于点P.
如图,ABCD-A1B1C1D1是正方体,O、M、N分别是B1D1、AB1、AD1的中点,直线A1C交平面AB1D1于点P.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
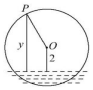 如图一半径为3米的水轮,水轮的圆心O距离水面2米,已知水轮每分钟旋转4圈,水轮上的点P到水面的距离y(米)与时间x(秒)满足函数关系y=Asin(ωx+φ)+2则有( )
如图一半径为3米的水轮,水轮的圆心O距离水面2米,已知水轮每分钟旋转4圈,水轮上的点P到水面的距离y(米)与时间x(秒)满足函数关系y=Asin(ωx+φ)+2则有( )| A. | ω=$\frac{2π}{15}$,A=3 | B. | ω=$\frac{2π}{15}$,A=5 | C. | ω=$\frac{15π}{2}$,A=5 | D. | ω=$\frac{15π}{2}$,A=3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{2}$) | B. | (-∞,1) | C. | (-∞,2) | D. | (-∞,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | $[\frac{1}{2},1]$ | C. | (-∞,0)∪$[\frac{1}{2},1]$ | D. | $(-\frac{1}{2},0]$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com