
 展开式的前三项系数成等差数列.则(1)n= ;(2)展开式的一次项是 ;(3)展开式中的有理项是 .
展开式的前三项系数成等差数列.则(1)n= ;(2)展开式的一次项是 ;(3)展开式中的有理项是 .  展开式的前三项系数成等差数列,
展开式的前三项系数成等差数列, +
+
 =2
=2 ×
× ,
, ×
× =n,
=n,
 ×
×
 =
=

 ,
, r=1得r=4.
r=1得r=4.
 x=
x= ×
× x=
x= x,
x, x.
x. r∈Z时,Tr+1为有理项,因为0≤r≤8且r∈Z,
r∈Z时,Tr+1为有理项,因为0≤r≤8且r∈Z, x,T9=
x,T9= x-2.
x-2. x;(3)x4,
x;(3)x4, x,
x, x-2.
x-2.

科目:高中数学 来源:2010年重庆市高二下学期期中考试数学(文) 题型:解答题
16.
(本小题满分13分) 已知 展开式的前三项系数成等差数列.
展开式的前三项系数成等差数列.
(1) 求n的值;
(2) 求展开式中二项式系数最大的项;
(3) 求展开式中系数最大的项.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 (1)已知
(1)已知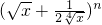 展开式的前三项系数成等差数列.求n.
展开式的前三项系数成等差数列.求n. 围成一个叶形图(阴影部分),向正方形AOBC内随机投一点(该点落在正方形AOBC内任何一点是等可能的),求所投的点落在叶形图内部的概率.
围成一个叶形图(阴影部分),向正方形AOBC内随机投一点(该点落在正方形AOBC内任何一点是等可能的),求所投的点落在叶形图内部的概率.查看答案和解析>>
科目:高中数学 来源:2009-2010学年重庆市西南师大附中高二(下)期中数学试卷(文科)(解析版) 题型:解答题
 展开式的前三项系数成等差数列.
展开式的前三项系数成等差数列.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com