
【题目】如图,在四棱锥![]() 中,
中, ![]() 底面
底面![]() ,底面
,底面![]() 为矩形,且
为矩形,且![]() ,
, ![]() 为
为![]() 的中点.
的中点.
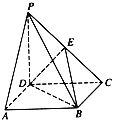
(1)过点![]() 作一条射线
作一条射线![]() ,使得
,使得![]() ,求证:平面
,求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正切值.
的正切值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)由题意画出图形,连接AC交BD于F,连接FE,由底面ABCD为矩形,得F为AC的中点,又E为PC的中点,利用三角形中位线定理可得EF∥PA,则PA∥平面BDE,再由AG∥BD,利用线面平行的判定可得AG∥平面BDE,结合面面平行的判定得平面PAG∥平面BDE;
(2)取CD的中点H,连接EH,则EH∥PD,因为PD⊥底面ABCD,所以EH⊥底面ABCD,
过H作MH⊥BD,垂足为M,连接EM,则∠EMH就是二面角E-BD-C的平面角,求出即可.
试题解析:
(1)在矩形ABCD中,连接AC,
设其与BD交于点O,连接OE,则O是AC的中点,
又E是PC的中点,所以 OE∥PA,
又![]() 平面BDE,
平面BDE, ![]() 平面BDE,所以PA∥平面BDE
平面BDE,所以PA∥平面BDE
同理AG∥平面BDE.
因为![]() AG=A,
AG=A,
所以平面PAG∥平面BDE.;
(2)取CD的中点H,连接EH,则EH∥PD,
因为PD⊥底面ABCD,所以EH⊥底面ABCD,
过H作MH⊥BD,垂足为M,连接EM,
则∠EMH就是二面角E-BD-C的平面角
令AD=1.则PD=1,AB=2,
在Rt△EMH中,易求得EH=![]() ,MH=
,MH=![]() ,
,
![]() ∠EMH=
∠EMH=![]()
所以二角面E-BD-C的正切值为![]()



 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足f(-x-1)=f(x-1),其图象过点(0,1),且与x轴有唯一交点。
(1)求f(x)的解析式;
(2)设函数g(x)=f(x)-(2+a)x,求g(x)在[1,2]上的最小值h(a)。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂2万元设计了某款式的服装,根据经验,每生产1百套该款式服装的成本为1万元,每生产![]() (百套)的销售额(单位:万元)
(百套)的销售额(单位:万元)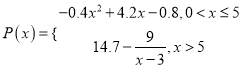 .
.
(1)若生产6百套此款服装,求该厂获得的利润;
(2)该厂至少生产多少套此款式服装才可以不亏本?
(3)试确定该厂生产多少套此款式服装可使利润最大,并求最大利润.(注:利润=销售额-成本,其中成本=设计费+生产成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面ABCD为矩形,PA⊥平面ABCD,点E是棱PD的中点,点F是PC的中点. (Ⅰ)证明:PB∥平面AEC;
(Ⅱ)若底面ABCD为正方形, ![]() ,求二面角C﹣AF﹣D大小.
,求二面角C﹣AF﹣D大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等腰梯形![]() 中(如图1),
中(如图1),![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 边上一点,且
边上一点,且![]() ,将
,将![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() (如图2).
(如图2).

(1)证明:平面![]() 平面
平面![]() ;
;
(2)试在棱![]() 上确定一点
上确定一点![]() ,使截面
,使截面![]() 把几何体分成的两部分
把几何体分成的两部分![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了普及环保知识,增强学生的环保意识,在全校组织了一次有关环保知识的竞赛.经过初赛、复赛,甲、乙两个代表队(每队3人)进入了决赛,规定每人回答一个问题,答对为本队赢得10分,答错得0分.假设甲队中每人答对的概率均为 ![]() ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为 ![]() ,
, ![]() ,
, ![]() ,且各人回答正确与否相互之间没有影响,用ξ表示乙队的总得分. (Ⅰ)求ξ的分布列和数学期望;
,且各人回答正确与否相互之间没有影响,用ξ表示乙队的总得分. (Ⅰ)求ξ的分布列和数学期望;
(Ⅱ)求甲、乙两队总得分之和等于30分且甲队获胜的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)在定义域[-1,1]上既是奇函数,又是减函数.
(1)求证:对任意x1,x2∈[-1,1],有[f(x1)+f(x2)]·(x1+x2)≤0;
(2)若f(1-a)+f(1-a2)<0,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com