
【题目】已知函数f(x)=log2(16x+k)﹣2x (k∈R)是偶函数.
(1)求k;
(2)若不等式m﹣1≤f(x)≤2m+log217在x∈[﹣1, ![]() ]上恒成立,求实数m的取值范围.
]上恒成立,求实数m的取值范围.
【答案】
(1)解:∵f(x)=log2(16x+k)﹣2x=log2(4x+ ![]() ),
),
∴f(﹣x)=log2(4﹣x+ ![]() )=log2(k4x+4﹣x),
)=log2(k4x+4﹣x),
由f(﹣x)=f(x)恒成立,得k=1
(2)解:∵log2(4x+4﹣x),令t=4x,由x∈[﹣1, ![]() ],
],
∴t∈[ ![]() ,2],
,2],
∵函数y=t+ ![]() 在[
在[ ![]() ,1]上单调递增,在[1,2]上单调递减,
,1]上单调递增,在[1,2]上单调递减,
∴当t=1时,即x=0时,函数f(x)有最小值f(0)=1,
∴当t= ![]() 时,即x=﹣1时,函数f(x)有最大值f(﹣1)=log2
时,即x=﹣1时,函数f(x)有最大值f(﹣1)=log2 ![]() ,
,
∵m﹣1≤f(x)≤2m+log217在x∈[﹣1, ![]() ]上恒成立,
]上恒成立,
∴m﹣1≤1且log2 ![]() ≤2m+log217.
≤2m+log217.
解得﹣1≤m≤2
故m的取值范围为[﹣1,2]
【解析】(1)由偶函数的定义f(﹣x)=f(x)恒成立可求;(2)不等式m﹣1≤f(x)≤2m+log217在x∈[﹣1, ![]() ]上恒成立,求出函数f(x)最值即可.
]上恒成立,求出函数f(x)最值即可.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
(1函数f(x)=loga(2x﹣1)﹣1的图象过定点(1,0);
(2化简2 ![]() +lg5lg2+(lg2)2﹣lg2的结果为25;
+lg5lg2+(lg2)2﹣lg2的结果为25;
(3若loga ![]() <1,则a的取值范围是(1,+∞);
<1,则a的取值范围是(1,+∞);
(4若2﹣x﹣2y>lnx﹣ln(﹣y)(x>0,y<0),则x+y<0.
其中所有正确命题的序号是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+θ)( A>0,ω>0,|θ|< ![]() )的最小正周期为π,且图象上有一个最低点为M(
)的最小正周期为π,且图象上有一个最低点为M( ![]() ,﹣3).
,﹣3).
(1)求f(x)的解析式;
(2)求函数f(x)在[0,π]的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿场售价与上市时间的关系如图一的一条折线表示;西红柿的种植成本与上市时间的关系如图二的抛物线段表示. 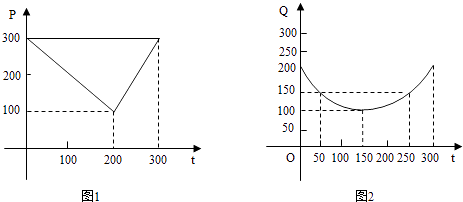
(1)写出图一表示的市场售价与时间的函数关系式p=f(t);写出图二表示的种植成本与时间的函数关系式Q=g(t);
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?(注:市场售价各种植成本的单位:元/102㎏,时间单位:天)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)上的一点M的横坐标为3,焦点为F,且|MF|=4.直线l:y=2x﹣4与抛物线C交于A,B两点.
(Ⅰ)求抛物线C的方程;
(Ⅱ)若P是x轴上一点,且△PAB的面积等于9,求点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cosxsin(x﹣ ![]() )+
)+ ![]() .
.
(1)求函数f(x)的对称轴方程;
(2)若方程sin2x+2|f(x+ ![]() )|﹣m+1=0在x∈[﹣
)|﹣m+1=0在x∈[﹣ ![]() ,
, ![]() ]上有三个实数解,求实数m的取值范围.
]上有三个实数解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=![]() ,AC=3, BC=2,P是△ABC内的一点.
,AC=3, BC=2,P是△ABC内的一点.
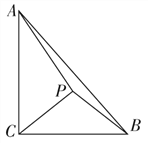
(1)若P是等腰直角三角形PBC的直角顶点,求PA的长;
(2)若∠BPC=![]() ,设∠PCB=θ,求△PBC的面积S(θ)的解析式,并求S(θ)的最大值.
,设∠PCB=θ,求△PBC的面积S(θ)的解析式,并求S(θ)的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com