
【题目】如图所示的立体图形中,![]() ,
,![]() .
.
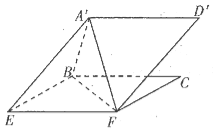
(Ⅰ)证明:![]()
![]()
![]() ;
;
(Ⅱ)若![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)证明见解析;(Ⅱ)![]()
【解析】
试题分析:(Ⅰ)要证![]()
![]()
![]() ,只需证
,只需证![]() 平面
平面![]() ,要证
,要证![]() 平面
平面![]() ,只需证明
,只需证明![]() 垂直于平面
垂直于平面![]() 两条相交直线即可,取
两条相交直线即可,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,由题意可得
,由题意可得![]()
![]() ,
,
再写出证明的过程即可
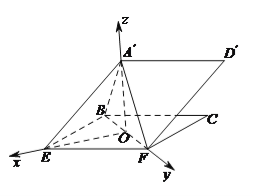
(Ⅱ)由题目中的垂直关系建立以![]() 为原点,直线
为原点,直线![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴
轴
建立空间直角坐标系![]() ,写出需要的点的坐标,再求得平面
,写出需要的点的坐标,再求得平面![]() 的一个法向量,易知
的一个法向量,易知![]() 是平面
是平面![]() 的一个法向量,求出两法向量的夹角的余弦值,由于因为二面角
的一个法向量,求出两法向量的夹角的余弦值,由于因为二面角![]() 为锐角,故二面角
为锐角,故二面角![]() 的余弦值为
的余弦值为![]() .
.
试题解析:(Ⅰ)证明:在图2中取![]() 的中点
的中点![]() ,
,
连接![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,
,
又因为![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
而![]() 平面
平面![]() ,所以
,所以![]()
![]()
![]() .
.
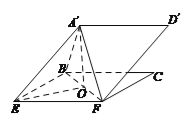
(Ⅱ)由(Ⅰ)知![]() ,
,![]() ,
,
因为![]() ,
,![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() 为等腰直角三角形,且
为等腰直角三角形,且![]() ,
,![]() ,
,
所以![]() ,
,
以![]() 为原点,直线
为原点,直线![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴
轴
建立空间直角坐标系![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,可求得平面
,可求得平面![]() 的一个法向量为
的一个法向量为![]() ,
,
易知![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
所以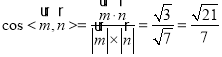 ,
,
因为二面角![]() 为锐角,故二面角
为锐角,故二面角![]() 的余弦值为
的余弦值为![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测4月和5月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过1000万?
相关公式:
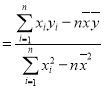 ,
,![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位共有10名员工,他们某年的收入如下表:
员工编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
年薪(万元) | 3 | 3.5 | 4 | 5 | 5.5 | 6.5 | 7 | 7.5 | 8 | 50 |
(1)从该单位中任取2人,此2人中年薪收入高于5万的人数记为![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
(2)已知员工年薪收入![]() 与工作所限
与工作所限![]() 成正相关关系,某员工工作第一年至第四年的年薪如下表:
成正相关关系,某员工工作第一年至第四年的年薪如下表:
工作年限 | 1 | 2 | 3 | 4 |
年薪(万元) | 3.0 | 4.2 | 5.6 | 7.2 |
预测该员工第五年的年薪为多少?
附:线性回归方程![]() 中系数计算公式和参考数据分别为:
中系数计算公式和参考数据分别为:
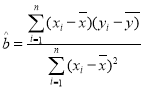 ,
,![]() ,其中
,其中![]() 为样本均值,
为样本均值,![]() ,
,![]() ,(
,(![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a1,d为实数,首项为a1,公差为d的等差数列{an}的前n项和为Sn,满足S5S6+15=0.
(1)若S5=5,求S6及a1;
(2)求d的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某化工厂近期要生产一批化工试剂,经市场调査得知,生产这批试剂厂家的生产成本有以下三个部分:①生产![]() 单位试剂需要原料费
单位试剂需要原料费![]() 元; ②支付所有职工的工资总额由
元; ②支付所有职工的工资总额由![]() 元的基本工资和每生产
元的基本工资和每生产![]() 单位试剂补貼所有职工
单位试剂补貼所有职工![]() 元组成; ③后续保养的平均费用是每单位
元组成; ③后续保养的平均费用是每单位![]() 元(试剂的总产量为
元(试剂的总产量为![]() 单位,
单位,![]() ).
).
(1)把生产每单位试剂的成本表示为![]() 的函数关系
的函数关系![]() ,并求出
,并求出![]() 的最小值;
的最小值;
(2)如果产品全部卖出,据测算销售額![]() (元)关于产量
(元)关于产量![]() (单位)的函数关系为
(单位)的函数关系为![]() ,试问:当产量为多少时生产这批试剂的利润最高?
,试问:当产量为多少时生产这批试剂的利润最高?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com