
【题目】如图,有一张半径为1米的圆形铁皮,工人师傅需要剪一块顶角为锐角的等腰三角形![]() ,不妨设
,不妨设 ![]() ,
, ![]() 边上的高为
边上的高为 ![]() ,圆心为
,圆心为 ![]() ,为了使三角形的面积最大,我们设计了两种方案.
,为了使三角形的面积最大,我们设计了两种方案.

(1)方案1:设 ![]() 为
为 ![]() ,用
,用![]() 表示
表示 ![]() 的面积
的面积 ![]() ; 方案2:设
; 方案2:设![]() 的高
的高![]() 为
为![]() ,用
,用![]() 表示
表示 ![]() 的面积
的面积![]() ;
;
(2)请从(1)中的两种方案中选择一种,求出![]() 面积的最大值
面积的最大值
科目:高中数学 来源: 题型:
【题目】学生学习的自律性很重要.某学校对自律性与学生成绩是否有关进行了调研,从该校学生中随机抽取了100名学生,通过调查统计得到![]() 列联表的部分数据如下表:
列联表的部分数据如下表:
自律性一般 | 自律性强 | 合计 | |
成绩优秀 | 40 | ||
成绩一般 | 20 | ||
合计 | 50 | 100 |
(1)补全![]() 列联表中的数据;
列联表中的数据;
(2)判断是否有![]() 的把握认为学生的自律性与学生成绩有关.
的把握认为学生的自律性与学生成绩有关.
参考公式及数据: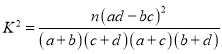 .
.
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是整数,幂函数
是整数,幂函数![]() 在
在![]() 上是单调递增函数.
上是单调递增函数.

(1)求幂函数![]() 的解析式;
的解析式;
(2)作出函数![]() 的大致图象;
的大致图象;
(3)写出![]() 的单调区间,并用定义法证明
的单调区间,并用定义法证明![]() 在区间
在区间![]() 上的单调性.
上的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①“三个球全部放入两个盒子,其中必有一个盒子有一个以上的球”是必然事件;②“当![]() 为某一实数时,可使
为某一实数时,可使![]() ”是不可能事件;③“明天兰州要下雨”是必然事件;④“从100个灯泡中取出5个,5个都是次品”是随机事件.
”是不可能事件;③“明天兰州要下雨”是必然事件;④“从100个灯泡中取出5个,5个都是次品”是随机事件.
其中正确命题的序号是( )
A.①②③④B.①②③C.①②④D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论中不正确的是( )
A.若两个平面有一个公共点,则它们有无数个公共点
B.若已知四个点不共面,则其中任意三点不共线
C.若点![]() 既在平面
既在平面![]() 内,又在平面
内,又在平面![]() 内,则
内,则![]() 与
与![]() 相交于
相交于![]() ,且点
,且点![]() 在
在![]() 上
上
D.任意两条直线不能确定一个平面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天干地支纪年法,源于中国中国自古便有十天干与十二地支十天干即甲、乙、丙、丁、戊、己、庚、辛、壬、癸,十二地支即子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥天干地支纪年法是按顺序以一个天干和一个地支相配,排列起来,天干在前,地支在后,天干由“甲”起,地支由“子”起,比如说第一年为“甲子”,第二年为“乙丑”,第三年为“丙寅”![]() 依此类推,排列到“癸酉”后,天干回到“甲”重新开始,即“甲戌”“乙亥”,之后地支回到“子”重新开始,即“丙子”
依此类推,排列到“癸酉”后,天干回到“甲”重新开始,即“甲戌”“乙亥”,之后地支回到“子”重新开始,即“丙子”![]() 依此类推已知1949年为“己丑”年,那么到新中国成立80周年时,即2029年为( )
依此类推已知1949年为“己丑”年,那么到新中国成立80周年时,即2029年为( )
A.己丑年B.己酉年C.壬巳年D.辛未年
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() .已知函数
.已知函数![]() ,
,![]() .
.
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)已知函数![]() 和
和![]() 的图象在公共点(x0,y0)处有相同的切线,
的图象在公共点(x0,y0)处有相同的切线,
(i)求证:![]() 在
在![]() 处的导数等于0;
处的导数等于0;
(ii)若关于x的不等式![]() 在区间
在区间![]() 上恒成立,求b的取值范围.
上恒成立,求b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com