
分析 (Ⅰ)由题意可得$A(-\sqrt{3},0),B(\sqrt{3},0)$,再设点P(x,y)(y≠0),从而可得$\frac{x^2}{3}+\frac{y^2}{2}=1$,从而化简${k_{PA}}•{k_{PB}}=\frac{y}{{x+\sqrt{3}}}•\frac{y}{{x-\sqrt{3}}}=\frac{y^2}{{{x^2}-3}}$,从而解得.
(Ⅱ)设M(x1,y1),N(x2,y2),设直线${l_{MN}}:x=ty-\frac{{\sqrt{3}}}{5}(t∈R)$,从而联立可得$(2{t^2}+3){y^2}-\frac{{4\sqrt{3}}}{5}ty-\frac{144}{25}=0$;结合韦达定理化简证明即可.
解答 解:(Ⅰ)$A(-\sqrt{3},0),B(\sqrt{3},0)$.设点P(x,y)(y≠0),
则有$\frac{x^2}{3}+\frac{y^2}{2}=1$,
即${y^2}=2(1-\frac{x^2}{3})=\frac{2}{3}(3-{x^2})$,
∴${k_{PA}}•{k_{PB}}=\frac{y}{{x+\sqrt{3}}}•\frac{y}{{x-\sqrt{3}}}=\frac{y^2}{{{x^2}-3}}$=$\frac{{\frac{2}{3}(3-{x^2})}}{{{x^2}-3}}=-\frac{2}{3}$.
(Ⅱ)证明:设M(x1,y1),N(x2,y2),
∵MN与x轴不重合,
∴设直线${l_{MN}}:x=ty-\frac{{\sqrt{3}}}{5}(t∈R)$,
由$\left\{\begin{array}{l}x=ty-\frac{{\sqrt{3}}}{5}\\ 2{x^2}+3{y^2}-6=0\end{array}\right.$化简得,
$(2{t^2}+3){y^2}-\frac{{4\sqrt{3}}}{5}ty-\frac{144}{25}=0$;
由题意可知△>0成立,且$\left\{\begin{array}{l}{y_1}+{y_2}=\frac{{\frac{{4\sqrt{3}}}{5}t}}{{2{t^2}+3}}\\{y_1}{y_2}=\frac{{-\frac{144}{25}}}{{2{t^2}+3}}\end{array}\right.$;
$\overrightarrow{AM}•\overrightarrow{AN}=({x_1}+\sqrt{3},{y_1})({x_2}+\sqrt{3},{y_2})=(t{y_1}+\frac{{4\sqrt{3}}}{5})(t{y_2}+\frac{{4\sqrt{3}}}{5})+{y_1}{y_2}$
=$({t^2}+1){y_1}{y_2}+\frac{{4\sqrt{3}}}{5}t({y_1}+{y_2})+\frac{48}{25}$;
将$\left\{\begin{array}{l}{y_1}+{y_2}=\frac{{\frac{{4\sqrt{3}}}{5}t}}{{2{t^2}+3}}\\{y_1}{y_2}=\frac{{-\frac{144}{25}}}{{2{t^2}+3}}\end{array}\right.$代入上式并化简得,
$\overrightarrow{AM}•\overrightarrow{AN}=\frac{{-\frac{144}{25}{t^2}-\frac{144}{25}+\frac{48}{25}{t^2}}}{{2{t^2}+3}}+\frac{48}{25}=-\frac{48}{25}×\frac{{2{t^2}+3}}{{2{t^2}+3}}+\frac{48}{25}=0$.
∴AM⊥AN,即以MN为直径的圆恒过点A.
点评 本题考查了椭圆与直线的位置关系的判断与应用,同时考查了韦达定理的应用及向量的应用.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:解答题
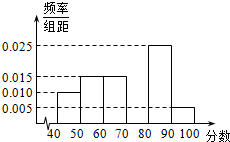 某校从参加高一年级期末考试的学生中抽出60名学生,将其数学成绩(满分100分,均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.根据图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出60名学生,将其数学成绩(满分100分,均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.根据图形的信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com