
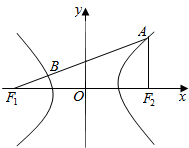
 已知双曲线中心在原点,焦点在x轴上,过左焦点F1作倾斜角为30°的直线l,交双曲线于A,B两点,F2为双曲线的右焦点,且AF2⊥x轴,如图.
已知双曲线中心在原点,焦点在x轴上,过左焦点F1作倾斜角为30°的直线l,交双曲线于A,B两点,F2为双曲线的右焦点,且AF2⊥x轴,如图.分析 (Ⅰ)将x=c代入双曲线方程求出点M的坐标,通过解直角三角形列出三参数a,b,c的关系,求出离心率的值;
(Ⅱ)设双曲线的方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{2{a}^{2}}$=1,直线AB的方程,代入双曲线方程,求出A,B的坐标,求出线段AB的长,利用|AB|=16,求双曲线的标准方程.
解答 解:(Ⅰ)将x=c代入双曲线的方程得y=±$\frac{{b}^{2}}{a}$,A(c,$\frac{{b}^{2}}{a}$)
在△AF1F2中tan30°=$\frac{\frac{{b}^{2}}{a}}{2c}$
即$\frac{{c}^{2}-{a}^{2}}{2ac}$=$\frac{\sqrt{3}}{3}$,解得e=$\frac{c}{a}$=$\sqrt{3}$;
(Ⅱ)由(Ⅰ)得b=$\sqrt{2}$a,设双曲线的方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{2{a}^{2}}$=1,
设直线AB的方程为y=$\frac{\sqrt{3}}{3}$(x-$\sqrt{3}$a)
将其代入双曲线方程消去y得,5x2+2$\sqrt{3}$ax-9a2=0,解之得x1=-$\sqrt{3}$a,x2=$\frac{3\sqrt{3}}{5}$a
将x1,x2代入①,得y1=-2a,y2=-$\frac{2}{5}$a,故A(-$\sqrt{3}$a,-2a),B($\frac{3\sqrt{3}}{5}$a,-$\frac{2}{5}$a),
故|AB|=$\sqrt{(-\frac{8\sqrt{3}}{5}a)^{2}+(\frac{8}{5}a)^{2}}$=$\frac{16}{5}$a=16,
∴a=5,
∴双曲线的方程为$\frac{{x}^{2}}{25}-\frac{{y}^{2}}{50}=1$.
点评 本题考查双曲线中三参数的关系:c2=a2+b2,考查双曲线的方程,考查直线与双曲线的位置关系,注意与椭圆中三参数关系的区别;求圆锥曲线的离心率就是求三参数的关系.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y2=4x或x2=$\frac{1}{2}$y | B. | y2=4x | C. | y2=4x或x2=-$\frac{1}{2}$y | D. | x2=-$\frac{1}{2}$y |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
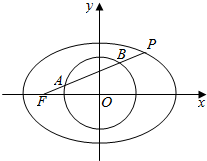 如图,过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点F作直线与圆x2+y2=$\frac{{a}^{2}}{4}$及椭圆依次交于点A、B、P,若FA=PB,且AB=$\frac{\sqrt{3}a}{2}$,则椭圆的离心率为$\frac{\sqrt{10}}{4}$.
如图,过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点F作直线与圆x2+y2=$\frac{{a}^{2}}{4}$及椭圆依次交于点A、B、P,若FA=PB,且AB=$\frac{\sqrt{3}a}{2}$,则椭圆的离心率为$\frac{\sqrt{10}}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com