
”¾ĢāÄæ”æĖę×ųĒŹŠ»Æ”¢¹¤Ņµ»Æ½ų³Ģ¼ÓĖŁ£¬Ęū³µ¹¤ŅµæģĖŁ·¢Õ¹£¬¹ś¼ŹŌÓĶ¹©ĒóƬ¶ÜÖš²½¼ÓÉī£¬Č«ĒņĘųŗņ±äÅÆČÕŅęĆ÷ĻŌ.ŌŚ“Ė±³¾°ĻĀ£¬ŅŌ½ŚÄܼõÅÅĪŖÖŲŅŖÄæ±źµÄŠĀÄÜŌ“Ęū³µ¼¼Źõ²»¶ĻČ”µĆĶ»ĘĘ£¬²¢³ŹĻÖæģĖŁĶ»ĘĘ”¢¾ŗĻą·¢Õ¹µÄĢ¬ŹĘ.ŌŚ2015Äź10ŌĀ·Ż£¬¹ś¼Ņ·¢øÄĪÆµČ²æĪÆŌŚ”¶µē¶ÆĘū³µ³äµē»ł“”É菩·¢Õ¹ÖøÄĻ£Ø2015-2020Äź£©”·ÖŠŅŖĒ󣬊Ā½Ø×”Õ¬Åä½ØĶ£³µĪ»Ó¦100%½ØÉč³äµē»ł“”É菩»ņŌ¤Įō½ØÉč°²×°Ģõ¼ž£¬“óŠĶ¹«¹²½ØÖžĪļÅä½ØĶ£³µ³””¢Éē»į¹«¹²Ķ£³µ³”½ØÉč³äµē»ł“”É菩»ņŌ¤Įō½ØÉč°²×°Ģõ¼žµÄ³µĪ»±ČĄż²»µĶÓŚ10%£¬Ćæ2000Į¾µē¶ÆĘū³µÓ¦ÖĮÉŁÅäĢ×½ØÉčŅ»×ł¹«¹²³äµēÕ¾.
ĪŖ¹ÄĄųŠĀÄÜŌ“Ęū³µ·¢Õ¹£¬¹ś¼ŅŗĶµŲ·½³öĢØĮĖĻą¹Ų²¹ĢłÕž²ß.
ø½±ķ1£ŗ2018ÄźÄ³ŹŠŠĀÄÜŌ“Ęū³µ²¹ĢłÕž²ß£ŗ
“æµēŠųŗ½Ąļ³Ģ£Ø | ¹ś¼Ņ²¹Ģł£ØĶņŌŖ/Į¾£© | µŲ·½²¹Ģł£ØĶņŌŖ/Į¾£© |
| 1.50 | 0.75 |
| 2.4 | 1.2 |
| 3.4 | 1.7 |
| 4.5 | 2.25 |
| 5 | 2.5 |
ĪŖĮĖ»ńµĆøü“óµÄŹŠ³”·Ö¶ī£¬ĒĄÕ¼Ī“Ą“ŠĀÄÜŌ“Ęū³µĻśŹŪĻČ»ś.øĆŹŠ¶Ō2018Äźø÷ĄąŠĶŠĀÄÜŌ“Ęū³µĻśŹŪÕ¼±ČĒéæö½ųŠŠĮĖµ÷²é.
ø½±ķ2£ŗ2018ÄźøĆŹŠø÷ĄąŠĶŠĀÄÜŌ“Ęū³µĻśŹŪÕ¼±ČĒéæö£ŗ
“æµēŠųŗ½Ąļ³Ģ |
|
|
|
|
|
Õ¼±Č | 5% | 20% | 35% | 25% | 15% |
£Ø1£©ÓĆ2018ÄźŠĀÄÜŌ“Ęū³µĻśŹŪÕ¼±ČĄ“¹Ą¼Ę2019ÄźµÄŠĀÄÜŌ“Ęū³µĻśŹŪĒéæö£¬Ēó2019ÄźĆæĮ¾ŠĀÄÜŌ“Ęū³µµÄĘ½¾ł²¹Ģł.ČōøĆŹŠ2019ÄźĻėŹµĻÖ3000ĶņŌŖ²¹Ģł£¬¹Ą¼ĘŠčŅŖĻśŹŪŠĀÄÜŌ“Ęū³µ¶ąÉŁĮæ.£Ø²¹ĢłÕž²ß°“ĆæĮ¾³µ²¹Ģł=¹ś¼Ņ²¹Ģł+µŲ·½²¹Ģł£¬½į¹ūĖÄÉįĪåČė±£ĮōÕūŹż£©
£Ø2£©øĆŹŠŠĀÄÜŌ“Ęū³µ“Ł½ų°ģ¹«±¦ĪŖĮĖµ÷²éŠĀÄÜŌ“Ęū³µ²¹Ģł·¢·ÅĒéæö£¬Ļ£Ķū“Ó2018ÄźĻśŹŪµÄŠĀÄÜĘÆŌ“Ęū³µÖŠ³éČ”10Į¾³µµÄŠÅĻ¢½ųŠŠ»Ų·ĆŗĖŹµ.ŅŌø÷ĄąŠĶŠĀÄÜŌ“Ęū³µĻśŹŪÕ¼±ČĪŖøÅĀŹ.Ēó³éµ½¼øĮ¾Šųŗ½Ąļ³ĢŠ”ÓŚ![]() ŠĀÄÜŌ“Ęū³µµÄæÉÄÜŠŌ×ī“ó.
ŠĀÄÜŌ“Ęū³µµÄæÉÄÜŠŌ×ī“ó.
”¾“š°ø”æ£Ø1£©5.45¼ū½āĪö£¬550Į¾£»£Ø2£©6Į¾
”¾½āĪö”æ
£Ø1£©øł¾ŻĢāŅāĮŠ³ö²¹ĢłµÄ·Ö²¼ĮŠ£¬øł¾ŻĘŚĶū¹«Ź½Ēó½ā£»
£Ø2£©Éč“ÓøĆ![]() µź³éČ”µÄ10Į¾³µÖŠŠųŗ½Ąļ³Ģ
µź³éČ”µÄ10Į¾³µÖŠŠųŗ½Ąļ³Ģ![]() Š”ÓŚ
Š”ÓŚ![]() ÓŠ
ÓŠ![]() Į¾£¬Ōņ
Į¾£¬Ōņ![]() £¬øł¾Ż¶žĻī·Ö²¼Ēó½ā.
£¬øł¾Ż¶žĻī·Ö²¼Ēó½ā.
£Ø1£©ÓÉĢāŅāÖŖĆæĮ¾³µµÄ²¹ĢłµÄ·Ö²¼ĮŠČēĻĀ±ķ£ŗ
| 2.25 | 3.6 | 5.1 | 6.75 | 7.5 |
| 5% | 20% | 35% | 25% | 15% |
Ōņ![]()
ŠčŅŖĻśŹŪŠĀÄÜŌ“Ęū³µĪŖ![]() £ØĮ¾£©
£ØĮ¾£©
£Ø2£©Éč“ÓøĆ![]() µź³éČ”µÄ10Į¾³µÖŠŠųŗ½Ąļ³Ģ
µź³éČ”µÄ10Į¾³µÖŠŠųŗ½Ąļ³Ģ![]() Š”ÓŚ
Š”ÓŚ![]() ÓŠ
ÓŠ![]() Į¾£¬Ōņ
Į¾£¬Ōņ![]() £¬
£¬
æÉÖŖ![]() £¬
£¬

½āµĆ![]()



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾£¬ŅŃÖŖ¶ąĆęĢåPABCDEµÄµ×ĆęABCDŹĒ±ß³¤ĪŖ2µÄĮāŠĪ£¬![]() µ×ĆęABCD£¬
µ×ĆęABCD£¬![]() £¬ĒŅ
£¬ĒŅ![]() .
.
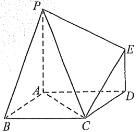
£Ø1£©Ö¤Ć÷£ŗĘ½Ćę![]() Ę½Ćę
Ę½Ćę![]() £»
£»
£Ø2£©Čō![]() £¬Ēó¶ąĆęĢå
£¬Ēó¶ąĆęĢå![]() µÄĢå»ż.
µÄĢå»ż.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æij³ĒŹŠŌŚ½ųŠŠ““½ØĪÄĆ÷³ĒŹŠµÄ»ī¶ÆÖŠ£¬ĪŖĮĖ½ā¾ÓĆń¶Ō”°““½ØĪÄĆ÷³Ē”±µÄĀśŅā³Ģ¶Č£¬×éÖƾÓĆńøų»ī¶Æ“ņ·Ö£Ø·ÖŹżĪŖÕūŹż£¬Āś·Ö100·Ö£©£¬“ÓÖŠĖ껜³éČ”Ņ»øöČŻĮæĪŖ120µÄŃł±¾£¬·¢ĻÖĖłøųŹż¾Ż¾łŌŚ[40£¬100]ÄŚ£®ĻÖ½«ÕāŠ©·ÖŹż·Ö³ÉŅŌĻĀ6×é²¢»³öŃł±¾µÄʵĀŹ·Ö²¼Ö±·½Ķ¼£¬µ«²»Š”ŠÄĪŪĖšĮĖ²æ·ÖĶ¼ŠĪ£¬ČēĶ¼ĖłŹ¾£®¹Ū²ģĶ¼ŠĪŌņĻĀĮŠĖµ·ØÖŠÓŠ“ķĪóµÄŹĒ£Ø £©
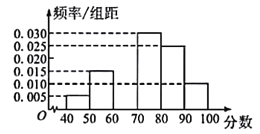
A.µŚČż×éµÄʵŹżĪŖ18ČĖ
B.øł¾ŻĘµĀŹ·Ö²¼Ö±·½Ķ¼¹Ą¼ĘÖŚŹżĪŖ75·Ö
C.øł¾ŻĘµĀŹ·Ö²¼Ö±·½Ķ¼¹Ą¼ĘŃł±¾µÄĘ½¾łŹżĪŖ75·Ö
D.øł¾ŻĘµĀŹ·Ö²¼Ö±·½Ķ¼¹Ą¼ĘŃł±¾µÄÖŠĪ»ŹżĪŖ75·Ö
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĖÄĄā׶S©ABCDÖŠ£¬²ąĆęSCDĪŖ¶Ū½ĒČż½ĒŠĪĒŅ“¹Ö±ÓŚµ×ĆęABCD£¬CD£½SD£¬µćMŹĒSAµÄÖŠµć£¬AD//BC£¬”ĻABC£½90”ć£¬AB£½AD![]() BC£½a£®
BC£½a£®

£Ø1£©ĒóÖ¤£ŗĘ½ĆęMBD”ĶĘ½ĆęSCD£»
£Ø2£©Čō”ĻSDC£½120”ć£¬ĒóČżĄā׶C©MBDµÄĢå»ż£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖÖ±Ļß![]() £ŗ
£ŗ![]() £¬°ė¾¶ĪŖ2µÄŌ²
£¬°ė¾¶ĪŖ2µÄŌ²![]() Óė
Óė![]() ĻąĒŠ£¬Ō²ŠÄ
ĻąĒŠ£¬Ō²ŠÄ![]() ŌŚ
ŌŚ![]() ÖįÉĻĒŅŌŚÖ±Ļß
ÖįÉĻĒŅŌŚÖ±Ļß![]() µÄÓŅÉĻ·½.
µÄÓŅÉĻ·½.

£Ø1£©ĒóŌ²![]() µÄ·½³Ģ£»
µÄ·½³Ģ£»
£Ø2£©¹żµć![]() µÄÖ±ĻßÓėŌ²
µÄÖ±ĻßÓėŌ²![]() ½»ÓŚ
½»ÓŚ![]() £¬
£¬![]() Į½µć£Ø
Į½µć£Ø![]() ŌŚ
ŌŚ![]() ÖįÉĻ·½£©£¬ĪŹŌŚ
ÖįÉĻ·½£©£¬ĪŹŌŚ![]() ÖįÕż°ėÖįÉĻŹĒ·ń“ęŌŚ¶Øµć
ÖįÕż°ėÖįÉĻŹĒ·ń“ęŌŚ¶Øµć![]() £¬Ź¹µĆ
£¬Ź¹µĆ![]() ÖįĘ½·Ö
ÖįĘ½·Ö![]() £æČō“ęŌŚ£¬ĒėĒó³öµć
£æČō“ęŌŚ£¬ĒėĒó³öµć![]() µÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ.
µÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬Ö±ĻßlµÄ²ĪŹż·½³ĢĪŖ![]() £ØtĪŖ²ĪŹż£©£¬ČōŅŌOĪŖ¼«µć£¬xÖįµÄÕż°ėÖįĪŖ¼«ÖįĒŅČ”ĻąĶ¬µÄµ„Ī»³¤¶Č½ØĮ¢¼«×ų±źĻµ£¬ĒśĻßCµÄ¼«×ų±ź·½³ĢĪŖ
£ØtĪŖ²ĪŹż£©£¬ČōŅŌOĪŖ¼«µć£¬xÖįµÄÕż°ėÖįĪŖ¼«ÖįĒŅČ”ĻąĶ¬µÄµ„Ī»³¤¶Č½ØĮ¢¼«×ų±źĻµ£¬ĒśĻßCµÄ¼«×ų±ź·½³ĢĪŖ![]() .
.
£Ø1£©ĒóĒśĻßCµÄÖ±½Ē×ų±ź·½³Ģ¼°Ö±ĻßlµÄĘÕĶØ·½³Ģ£»
£Ø2£©½«ĖłµĆĒśĻßCĻņÓŅĘ½ŅĘ1øöµ„Ī»³¤¶Č£¬ŌŁ½«ĒśĻßCÉĻµÄĖłÓŠµćµÄŗį×ų±ź±äĪŖŌĄ“µÄ2±¶£¬µĆµ½ĒśĻß![]() £¬ĒóĒśĻß
£¬ĒóĒśĻß![]() ÉĻµÄµćµ½Ö±ĻßlµÄ¾ąĄėµÄ×ī“óÖµ.
ÉĻµÄµćµ½Ö±ĻßlµÄ¾ąĄėµÄ×ī“óÖµ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČē¹ū¶Ōij¶ŌĻóĮ¬ŠųŹµŹ©Į½“Ī±ä»»ŗóµÄ½į¹ū¾ĶŹĒ±ä»»Ē°µÄ¶ŌĻó£¬ÄĒĆ“ĪŅĆĒ³ĘÕāÖֱ任ĪŖ”°»Ų¹é”±±ä»».Čē£ŗ¶ŌČĪŅāŅ»øöŹµŹż£¬±ä»»£ŗČ”ĘäĻą·“Źż.ŅņĪŖĻą·“ŹżµÄĻą·“ŹżŹĒĖü±¾Éķ£¬ĖłŅŌ±ä»»”°Č”ŹµŹżµÄĻą·“Źż”±ŹĒŅ»ÖÖ”°»Ų¹é”±±ä»».ÓŠĻĀĮŠ3Öֱ任£ŗ
¢Ł¶Ō![]() £¬±ä»»£ŗĒó¼ÆŗĻAµÄ²¹¼Æ£»
£¬±ä»»£ŗĒó¼ÆŗĻAµÄ²¹¼Æ£»
¢Ś¶ŌČĪŅā![]() £¬±ä»»£ŗĒózµÄ¹²éīø“Źż£»
£¬±ä»»£ŗĒózµÄ¹²éīø“Źż£»
¢Ū¶ŌČĪŅā![]() £¬±ä»»£ŗ
£¬±ä»»£ŗ![]() £Øk£¬b¾łĪŖ·ĒĮ揵Źż£©.
£Øk£¬b¾łĪŖ·ĒĮ揵Źż£©.
ĘäÖŠŹĒ”°»Ų¹é”±±ä»»µÄŹĒ______.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æij¹¤³§ĪŖĢįøßÉś²śŠ§ĀŹ£¬æŖÕ¹¼¼Źõ““ŠĀ»ī¶Æ£¬Ģį³öĮĖĶź³ÉijĻīÉś²śČĪĪńµÄĮ½ÖÖŠĀµÄÉś²ś·½Ź½£®ĪŖ±Č½ĻĮ½ÖÖÉś²ś·½Ź½µÄŠ§ĀŹ£¬Ń”Č”40Ćū¹¤ČĖ£¬½«ĖūĆĒĖ껜·Ö³ÉĮ½×飬Ćæ×é20ČĖ£¬µŚŅ»×鹤ČĖÓƵŚŅ»ÖÖÉś²ś·½Ź½£¬µŚ¶ž×鹤ČĖÓƵŚ¶žÖÖÉś²ś·½Ź½£®øł¾Ż¹¤ČĖĶź³ÉÉś²śČĪĪńµÄ¹¤×÷Ź±¼ä£Øµ„Ī»£ŗmin£©»ęÖĘĮĖ¾„Ņ¶Ķ¼£ŗŌņĻĀĮŠ½įĀŪÖŠ±ķŹö²»ÕżČ·µÄŹĒ
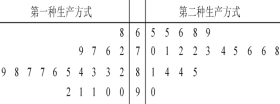
A. µŚŅ»ÖÖÉś²ś·½Ź½µÄ¹¤ČĖÖŠ£¬ÓŠ75%µÄ¹¤ČĖĶź³ÉÉś²śČĪĪńĖłŠčŅŖµÄŹ±¼äÖĮÉŁ80·ÖÖÓ
B. µŚ¶žÖÖÉś²ś·½Ź½±ČµŚŅ»ÖÖÉś²ś·½Ź½µÄŠ§ĀŹøüøß
C. Õā40Ćū¹¤ČĖĶź³ÉČĪĪńĖłŠčŹ±¼äµÄÖŠĪ»ŹżĪŖ80
D. ĪŽĀŪÄÄÖÖÉś²ś·½Ź½µÄ¹¤ČĖĶź³ÉÉś²śČĪĪńĘ½¾łĖłŠčŅŖµÄŹ±¼ä¶¼ŹĒ80·ÖÖÓ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŹżŃ§ÖŠÓŠŠķ¶ąŌ¢ŅāĆĄŗƵÄĒśĻߣ¬ĒśĻß![]() ±»³ĘĪŖ”°ĖÄŅ¶Ćµ¹åĻß”±£ØČēĶ¼ĖłŹ¾£©.
±»³ĘĪŖ”°ĖÄŅ¶Ćµ¹åĻß”±£ØČēĶ¼ĖłŹ¾£©.

øų³öĻĀĮŠČżøö½įĀŪ£ŗ
¢ŁĒśĻß![]() ¹ŲÓŚÖ±Ļß
¹ŲÓŚÖ±Ļß![]() ¶Ō³Ę£»
¶Ō³Ę£»
¢ŚĒśĻß![]() ÉĻČĪŅāŅ»µćµ½ŌµćµÄ¾ąĄė¶¼²»³¬¹ż
ÉĻČĪŅāŅ»µćµ½ŌµćµÄ¾ąĄė¶¼²»³¬¹ż![]() £»
£»
¢Ū“ęŌŚŅ»øöŅŌŌµćĪŖÖŠŠÄ”¢±ß³¤ĪŖ![]() µÄÕż·½ŠĪ£¬Ź¹µĆĒśĻß
µÄÕż·½ŠĪ£¬Ź¹µĆĒśĻß![]() ŌŚ“ĖÕż·½ŠĪĒųÓņÄŚ£Øŗ¬±ß½ē£©.
ŌŚ“ĖÕż·½ŠĪĒųÓņÄŚ£Øŗ¬±ß½ē£©.
ĘäÖŠ£¬ÕżČ·½įĀŪµÄŠņŗÅŹĒ________.
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com