Question

在等比数列{a_n} 中，若a₁和a₂是一元二次方程x²-4x+3=0的两个根，则a₅等于（ ）
A．
B．81
C．81或
D．81或

Answer 1

【答案】分析：法一：由a₁和a₂是一元二次方程x²-4x+3=0的两个根，利用韦达定理求出两个之和与两根之积，联立求出方程的两个根，得出a₁和a₂的值，但是a₁和a₂的大小未知，故分两种情况考虑，a₁和a₂是1和3，或3和1，利用等比数列的性质求出公比的值，根据等比数列的通项公式即可求出a₅的值；
法二：利用分解因式法求出已知一元二次方程的解，可得出a₁和a₂的值，根据a₁和a₂的大小未知，分两种情况考虑，a₁和a₂是1和3，或3和1，利用等比数列的性质求出公比的值，根据等比数列的通项公式即可求出a₅的值．
解答：解：法一：∵a₁和a₂是一元二次方程x²-4x+3=0的两个根，
∴a₁+a₂=4，a₁a₂=3，
∴a₁=1，a₂=3，或a₁=3，a₂=1，
∴公比q=3或，
则a₅=a₁q⁴=81或；
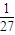
法二：x²-4x+3=0，
可化为：（x-1）（x-3）=0，
解得：x₁=1，x₂=3，
∴a₁=1，a₂=3，或a₁=3，a₂=1，
∴公比q=3或，
则a₅=a₁q⁴=81或．
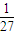
故选D
点评：此题考查了一元二次方程的解法，韦达定理，等比数列的性质，以及等比数列的通项公式，利用分类讨论的数学思想，由于a₁和a₂的大小未知，故分两种情况考虑．
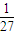
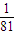
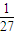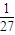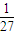