
【题目】在平面直角坐标系![]() ,
,![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,已知曲线
轴正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 为
为![]() 上的动点,
上的动点,![]() 为
为![]() 的中点.
的中点.
(1)请求出![]() 点轨迹
点轨迹![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的极坐标为
的极坐标为![]() 若直线
若直线![]() 经过点
经过点![]() 且与曲线
且与曲线![]() 交于点
交于点![]() ,弦
,弦![]() 的中点为
的中点为![]() ,求
,求![]() 的取值范围.
的取值范围.
 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
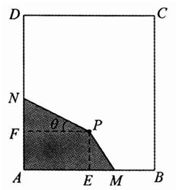
【题目】(题文)如图,长方形材料![]() 中,已知
中,已知![]() ,
,![]() .点
.点![]() 为材料
为材料![]() 内部一点,
内部一点,![]() 于
于![]() ,
,![]() 于
于![]() ,且
,且![]() ,
,![]() . 现要在长方形材料
. 现要在长方形材料![]() 中裁剪出四边形材料
中裁剪出四边形材料![]() ,满足
,满足![]() ,点
,点![]() 、
、![]() 分别在边
分别在边![]() ,
,![]() 上.
上.
(1)设![]() ,试将四边形材料
,试将四边形材料![]() 的面积表示为
的面积表示为![]() 的函数,并指明
的函数,并指明![]() 的取值范围;
的取值范围;
(2)试确定点![]() 在
在![]() 上的位置,使得四边形材料
上的位置,使得四边形材料![]() 的面积
的面积![]() 最小,并求出其最小值.
最小,并求出其最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 为抛物线
为抛物线![]() 上一点.
上一点.
(1)若![]() ,求
,求![]()
(2)已知点![]() ,过点
,过点![]() 作直线
作直线![]() 分别交曲线
分别交曲线![]() 于
于![]() ,证明:在点
,证明:在点![]() 运动过程中,直线
运动过程中,直线![]() 始终过定点,并求出该定点.
始终过定点,并求出该定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】绝大部分人都有患呼吸系统疾病的经历,现在我们调查患呼吸系统疾病是否和所处环境有关.一共调查了![]() 人,患有呼吸系统疾病的
人,患有呼吸系统疾病的![]() 人,其中
人,其中![]() 人在室外工作,
人在室外工作,![]() 人在室内工作.没有患呼吸系统疾病的
人在室内工作.没有患呼吸系统疾病的![]() 人,其中
人,其中![]() 人在室外工作,
人在室外工作,![]() 人在室内工作.
人在室内工作.
(1)现采用分层抽样从室内工作的居民中抽取一个容量为![]() 的样本,将该样本看成一个总体,从中随机的抽取两人,求两人都有呼吸系统疾病的概率.
的样本,将该样本看成一个总体,从中随机的抽取两人,求两人都有呼吸系统疾病的概率.
(2)你能否在犯错误率不超过![]() 的前提下认为感染呼吸系统疾病与工作场所有关;
的前提下认为感染呼吸系统疾病与工作场所有关;
附表:
|
|
|
|
|
|
|
|
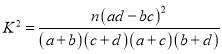
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆:![]() 的离心率为
的离心率为![]() ,y轴于椭圆相交于A、B两点,
,y轴于椭圆相交于A、B两点,![]() ,C、D是椭圆上异于A、B的任意两点,且直线AC、BD相交于点M,直线AD、BC相交于点N.
,C、D是椭圆上异于A、B的任意两点,且直线AC、BD相交于点M,直线AD、BC相交于点N.
![]() 求椭圆的方程;
求椭圆的方程;
![]() 求直线MN的斜率.
求直线MN的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() 上一点
上一点![]() 到左右两个焦点
到左右两个焦点![]() 的距离之和是4.
的距离之和是4.
(1)求椭圆的方程;
(2)已知过![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 两点,且两点与左右顶点不重合,若
两点,且两点与左右顶点不重合,若![]() ,求四边形
,求四边形![]() 面积的最大值。
面积的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某少数民族的刺绣有着悠久的历史,如图4①,②,③,④为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.

(1)求出f(5)的值;
(2)利用合情推理的“归纳推理思想”,归纳出f(n+1)与f(n)之间的关系式,并根据你得到的关系式求出f(n)的表达式;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知若椭圆![]() :
:![]() (
(![]() )交
)交![]() 轴于
轴于![]() ,
,![]() 两点,点
两点,点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() ,
,![]() 的任意一点,直线
的任意一点,直线![]() ,
,![]() 分别交
分别交![]() 轴于点
轴于点![]() ,
,![]() ,则
,则![]() 为定值
为定值![]() .
.
(1)若将双曲线与椭圆类比,试写出类比得到的命题;
(2)判定(1)类比得到命题的真假,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com