
| 喜欢网购 | 不喜欢网购 | 总计 | |
| 男职工 | |||
| 女职工 | |||
| 总计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)本题是一个简单的数字的运算,根据a,b,c,d的已知和未知的结果,做出空格处的结果.
(2)由已知数据可求得观测值,把求得的观测值同临界值进行比较,看能否在犯错误的概率不超过0.001的前提下认为喜欢网购与职工性别有关系.
解答 解:(1)依题意,2×2列联表为:
| 喜欢网购 | 不喜欢网购 | 总计 | |
| 男职工 | 10 | 50 | 60 |
| 女职工 | 20 | 10 | 30 |
| 总计 | 30 | 60 | 90QUOTE |
点评 本题考查独立性检验的列联表.考查假设性判断,解题的过程比较麻烦,但这种问题的解答原理比较简单,是一个送分题目.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$$\overrightarrow{a}$-$\frac{4}{5}$$\overrightarrow{b}$ | B. | $\frac{2}{5}$$\overrightarrow{a}$+$\frac{4}{5}$$\overrightarrow{b}$ | C. | -$\frac{2}{5}$$\overrightarrow{a}$+$\frac{4}{5}$$\overrightarrow{b}$ | D. | -$\frac{2}{5}$$\overrightarrow{a}$-$\frac{4}{5}$$\overrightarrow{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
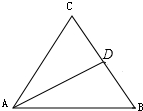 如图,在△ABC中,D为边BC的中点,则下列结论正确的是( )
如图,在△ABC中,D为边BC的中点,则下列结论正确的是( )| A. | $\overrightarrow{AB}$+$\overrightarrow{AC}$=$\overrightarrow{AD}$ | B. | $\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{BC}$ | C. | $\overrightarrow{AB}$+$\overrightarrow{DC}$=$\overrightarrow{AD}$ | D. | $\overrightarrow{AB}$-$\overrightarrow{DC}$=$\overrightarrow{BC}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 总计 | |
| 参加数学第二课堂活动 | p | ||
| 未参加数学第二课堂活动 | q | 100 | |
| 总计 | 200 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
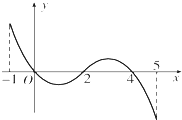 已知函数f(x)的定义域为[-1,5],f(x)的导函数f′(x)的图象如图所示.若f(x)在区间[m,m+1]上是单调函数,则实数m的取值范围是{m|m=-1或0≤m≤1或2≤m≤3或m=4}.
已知函数f(x)的定义域为[-1,5],f(x)的导函数f′(x)的图象如图所示.若f(x)在区间[m,m+1]上是单调函数,则实数m的取值范围是{m|m=-1或0≤m≤1或2≤m≤3或m=4}.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∨(¬q) | B. | p∧(¬q) | C. | p∨q | D. | p∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com