Question

（满分20分）本题有2小题，第1小题12分，第2小题8分．
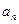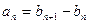已知数列{}和{}满足：对于任何，有，为非零常数），且．
（1）求数列{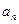}和{}的通项公式；
（2）若是与的等差中项，试求的值，并研究：对任意的，是否一定能是数列{}中某两项（不同于）的等差中项，并证明你的结论．

Answer 1

略

解析（1）【解一】由得，
．
又，，．
所以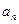，{}是首项为1，公比为的等比数列，．…………………………….5分
由，得

所以，当时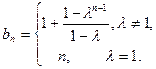，……………………………………………….6分
上式对显然成立．………………………………………………………………………..1分
【解二】猜测，并用数学归纳法证明…………………………………………….5分
的求法如【解一】  ………………………………………………………………………..7分
【解三】猜测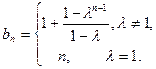，并用数学归纳法证明………………………….7分
  …………………………………………………………………..5分
（2）当时，不是与的等差中项，不合题意；……………………………….1分
当时，由得，
由得（可解得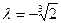）..…………………………………………2分
对任意的，是与的等差中项． .………………………………….2分
证明：，
，                    .………………………………….3分
即，对任意的，是与的等差中项．