
如果函数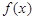 满足在集合
满足在集合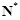 上的值域仍是集合
上的值域仍是集合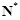 ,则把函数
,则把函数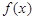 称为N函数.
称为N函数.
例如: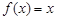 就是N函数.
就是N函数.
(Ⅰ)判断下列函数:①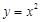 ,②
,②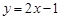 ,③
,③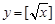 中,哪些是N函数?(只需写出判断结果);
中,哪些是N函数?(只需写出判断结果);
(Ⅱ)判断函数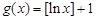 是否为N函数,并证明你的结论;
是否为N函数,并证明你的结论;
(Ⅲ)证明:对于任意实数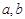 ,函数
,函数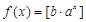 都不是N函数.
都不是N函数.
(注:“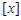 ”表示不超过
”表示不超过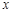 的最大整数)
的最大整数)
(Ⅰ)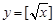 ;(Ⅱ)是N函数;(Ⅲ)略
;(Ⅱ)是N函数;(Ⅲ)略
【解析】
试题分析:(Ⅰ)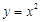 的定义域为
的定义域为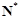 时,值域不是集合
时,值域不是集合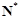 ,例如值域中不含2。故
,例如值域中不含2。故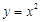 不是N函数 。
不是N函数 。 的定义域为
的定义域为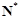 时,值域不是集合
时,值域不是集合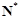 ,例如值域中不含2。故
,例如值域中不含2。故 不是N函数。当
不是N函数。当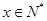 时
时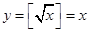 ,所以
,所以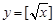 是N函数。(Ⅱ)因为“
是N函数。(Ⅱ)因为“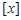 ”表示不超过
”表示不超过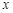 的最大整数,所以
的最大整数,所以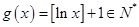 。设
。设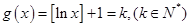 ,则
,则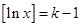 ,所以
,所以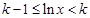 ,解得
,解得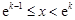 ,因为
,因为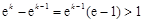 所以在
所以在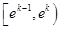 一定存在正整数
一定存在正整数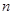 ,即存在
,即存在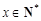 满足
满足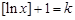 (Ⅲ)需对实数
(Ⅲ)需对实数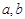 在全体实数范围内进行讨论。若
在全体实数范围内进行讨论。若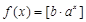 为负时,函数
为负时,函数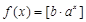 不是N函数;若函数
不是N函数;若函数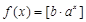 有最大值时,函数
有最大值时,函数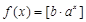 不是N函数;若函数
不是N函数;若函数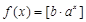 的值是正数但不能取到所有正数时,函数
的值是正数但不能取到所有正数时,函数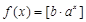 不是N函数。
不是N函数。
试题解析:解:(Ⅰ)只有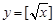 是N函数.
3分
是N函数.
3分
(Ⅱ)函数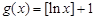 是N函数.
是N函数.
证明如下:
显然,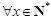 ,
, 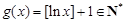 .
4分
.
4分
不妨设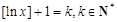 ,
,
由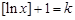 可得
可得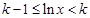 ,
,
即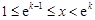 .
.
因为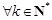 ,恒有
,恒有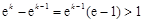 成立,
成立,
所以一定存在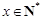 ,满足
,满足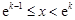 ,
,
所以设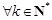 ,总存在
,总存在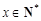 满足
满足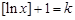 ,
,
所以函数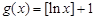 是N函数.
8分
是N函数.
8分
(Ⅲ)(1)当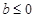 时,有
时,有 ,
,
所以函数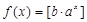 都不是N函数.
9分
都不是N函数.
9分
(2)当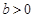 时,① 若
时,① 若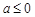 ,有
,有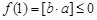 ,
,
所以函数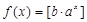 都不是N函数.
10分
都不是N函数.
10分
② 若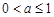 ,由指数函数性质易得
,由指数函数性质易得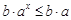 ,
,
所以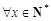 ,都有
,都有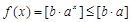
所以函数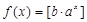 都不是N函数.
11分
都不是N函数.
11分
③ 若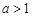 ,令
,令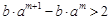 ,则
,则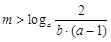 ,
,
所以一定存在正整数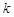 使得
使得
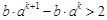 ,
,
所以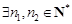 ,使得
,使得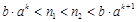 ,
,
所以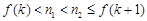 .
.
又因为当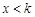 时,
时,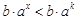 ,所以
,所以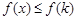 ;
;
当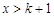 时,
时,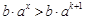 ,所以
,所以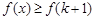 ,
,
所以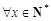 ,都有
,都有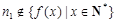 ,
,
所以函数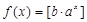 都不是N函数.
13分
都不是N函数.
13分
综上所述,对于任意实数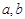 ,函数
,函数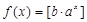 都不是N函数.
都不是N函数.
考点:新概念问题,考查分析能力、对所学知识的综合运用能力及论证推理能力。


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1-ax |
| x-1 |
| 5 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(06年广东卷)(12分)
A是由定义在![]() 上且满足如下条件的函数
上且满足如下条件的函数![]() 组成的集合:①对任意
组成的集合:①对任意![]() ,都有
,都有![]() ; ②存在常数
; ②存在常数![]() ,使得对任意的
,使得对任意的![]() ,都有
,都有![]()
(Ⅰ)设![]() ,证明:
,证明:![]()
(Ⅱ) 设![]() ,如果存在
,如果存在![]() ,使得
,使得![]() ,那么这样的
,那么这样的![]() 是唯一的;
是唯一的;
(Ⅲ) 设![]() ,任取
,任取![]() ,令
,令![]() 证明:给定正整数k,对任意的正整数p,成立不等式
证明:给定正整数k,对任意的正整数p,成立不等式![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com