
【题目】若直线![]() 与
与![]() 轴,
轴,![]() 轴的交点分别为
轴的交点分别为![]() ,圆
,圆![]() 以线段
以线段![]() 为直径.
为直径.
(Ⅰ)求圆![]() 的标准方程;
的标准方程;
(Ⅱ)若直线![]() 过点
过点![]() ,与圆
,与圆![]() 交于点
交于点![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
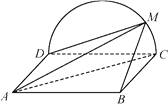
【题目】如图,边长为2的正方形![]() 所在的平面与半圆弧
所在的平面与半圆弧![]() 所在平面垂直,
所在平面垂直,![]() 是
是![]() 上异于
上异于![]() ,
,![]() 的点.
的点.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 体积最大时,求面
体积最大时,求面![]() 与面
与面![]() 所成二面角的正弦值.
所成二面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为![]() 的函数
的函数![]() ,若满足①
,若满足① ![]() ;② 当
;② 当![]() ,且
,且![]() 时,都有
时,都有![]() ;③ 当
;③ 当![]() ,且
,且![]() 时,都有
时,都有![]() ,则称
,则称![]() 为“偏对称函数”.现给出四个函数:①
为“偏对称函数”.现给出四个函数:①![]() ;②
;② ![]() ; ③
; ③![]() ;④
;④![]() .则其中是“偏对称函数”的函数序号为 _______.
.则其中是“偏对称函数”的函数序号为 _______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为比较甲、乙两地某月11时的气温情况,随机选取该月中的5天中11时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论:
①甲地该月11时的平均气温低于乙地该月11时的平均气温
②甲地该月11时的平均气温高于乙地该月11时的平均气温
③甲地该月11时的气温的标准差小于乙地该月11时的气温的标准差
④甲地该月11时的气温的标准差大于乙地该月11时的气温的标准差
其中根据茎叶图能得到的正确结论的编号为( )
A.①③
B.①④
C.②③
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为比较甲、乙两地某月11时的气温情况,随机选取该月中的5天中11时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论:
①甲地该月11时的平均气温低于乙地该月11时的平均气温
②甲地该月11时的平均气温高于乙地该月11时的平均气温
③甲地该月11时的气温的标准差小于乙地该月11时的气温的标准差
④甲地该月11时的气温的标准差大于乙地该月11时的气温的标准差
其中根据茎叶图能得到的正确结论的编号为( )
A.①③
B.①④
C.②③
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业有![]() 、
、![]() 两个岗位招聘大学毕业生,其中第一天收到这两个岗位投简历的大学生人数如下表:
两个岗位招聘大学毕业生,其中第一天收到这两个岗位投简历的大学生人数如下表:
|
| 总计 | |
女生 | 12 | 8 | 20 |
男生 | 24 | 56 | 80 |
总计 | 36 | 64 | 100 |
(1)根据以上数据判断是有![]() 的把握认为招聘的
的把握认为招聘的![]() 、
、![]() 两个岗位与性别有关?
两个岗位与性别有关?
(2)从投简历的女生中随机抽取两人,记其中投![]() 岗位的人数为
岗位的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
| 0.050 | 0.025 | 0.010 |
| 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现需要设计一个仓库,由上下两部分组成,上部的形状是正四棱锥![]() ,下部的形状是正四棱柱
,下部的形状是正四棱柱![]() (如图所示),并要求正四棱柱的高
(如图所示),并要求正四棱柱的高![]() 是正四棱锥的高
是正四棱锥的高![]() 的4倍.
的4倍.

(1)若![]() ,
,![]() ,则仓库的容积是多少?
,则仓库的容积是多少?
(2)若正四棱锥的侧棱长为![]() ,当
,当![]() 为多少时,下部的正四棱柱侧面积最大,最大面积是多少?
为多少时,下部的正四棱柱侧面积最大,最大面积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c.已知b=acosC+3bsin(B+C).
(1)若 ![]() ,求角A;
,求角A;
(2)在(1)的条件下,若△ABC的面积为 ![]() ,求a的值.
,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com