
【题目】若函数f(x)= ![]() x2﹣lnx在其定义域的一个子区间(k﹣1,k+1)上不是单调函数,则实数k的取值范围是( )
x2﹣lnx在其定义域的一个子区间(k﹣1,k+1)上不是单调函数,则实数k的取值范围是( )
A.(1,2)
B.[1,2)
C.[0,2)
D.(0,2)
【答案】B
【解析】解:函数的定义域为(0,+∞), ∴函数的f′(x)=x﹣ ![]() =
= ![]() ,
,
由f′(x)>0解得x>1,此时函数单调递增,
由f′(x)<0解得0<x<1,此时函数单调递减,
故x=1时,函数取得极小值.
①当k=1时,(k﹣1,k+1)为(0,2),函数在(0,1)上单调减,在(1,2)上单调增,此时函数在(0,2)上不是单调函数,满足题意;
②当k>1时,∵函数f(x)在其定义域的一个子区间(k﹣1,k+1)内不是单调函数,
∴x=1在(k﹣1,k+1)内,
即 ![]() ,即
,即 ![]() ,即0<k<2,
,即0<k<2,
此时1<k<2,
综上1≤k<2,
故选:B.
【考点精析】本题主要考查了利用导数研究函数的单调性的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能正确解答此题.
在这个区间单调递减才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的最大值;
的最大值;
(2)若对于任意![]() ,均有
,均有![]() ,求正实数
,求正实数![]() 的取值范围;
的取值范围;
(3)是否存在实数![]() ,使得不等式
,使得不等式![]() 对于任意
对于任意![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,已知 ![]() ,sinA=
,sinA= ![]() . (Ⅰ)求sinC的值;
. (Ⅰ)求sinC的值;
(II)设D为AC的中点,若△ABC的面积为8 ![]() ,求BD的长.
,求BD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选做题:几何证明选讲 如图,ABCD是边长为a的正方形,以D为圆心,DA为半径的圆弧与以BC为直径的半圆O交于点F,延长CF交AB于E.
(1)求证:E是AB的中点;
(2)求线段BF的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2x+2sinxcosx+3cos2x. (Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)若x∈[0, ![]() ],求函数f(x)的最值及相应x的取值.
],求函数f(x)的最值及相应x的取值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x-1|+|x-2|.
(1)求不等式f(x)≥3的解集;
(2)若存在实数x满足f(x)≤-a2+a+7,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次.得到甲、乙两位学生成绩的茎叶图.
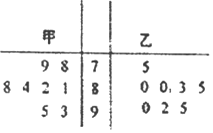
(1)现要从中选派一人参加数学竞赛,对预赛成绩的平均值和方差进行分析,你认为哪位学生的成绩更稳定?请说明理由;
(2)求在甲同学的8次预赛成绩中,从不小于80分的成绩中随机抽取2个成绩,列出所有结果,并求抽出的2个成绩均大于85分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义“规范01数列”![]() 如下:
如下:![]() 共有
共有![]() 项,其中
项,其中![]() 项为0,
项为0,![]() 项为1,且对任意
项为1,且对任意![]() ,
,![]() ,
,![]() ,…,
,…,![]() 中0的个数不少于1的个数.若
中0的个数不少于1的个数.若![]() ,则不同的“规范01数列”共有( )
,则不同的“规范01数列”共有( )
A. 14个 B. 13个 C. 15个 D. 12个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com