
【题目】某校高中生共有2700人,其中高一年级900人,高二年级1200人,高三年级600人,现采取分层抽样法抽取容量为135的样本,那么高一,高二,高三各年级抽取的人数分别为( )
A.45,75,15
B.45,45,45
C.30,90,15
D.45,60,30
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0 ) 经过点 P(1,
(a>b>0 ) 经过点 P(1, ![]() ),离心率 e=
),离心率 e= ![]()
(Ⅰ)求椭圆C的标准方程.
(Ⅱ)设过点E(0,﹣2 ) 的直线l 与C相交于P,Q两点,求△OPQ 面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{bn}满足bn=| ![]() |,其中a1=2,an+1=
|,其中a1=2,an+1= ![]() .
.
(1)求b1 , b2 , b3 , 并猜想bn的表达式(不必写出证明过程);
(2)由(1)写出数列{bn}的前n项和Sn , 并用数学归纳法证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,P是平行四边形ABCD所在平面外一点,E是PD的中点. 
(1)求证:PB∥平面EAC;
(2)若M是CD上异于C、D的点.连结PM交CE于G,连结BM交AC于H,求证:GH∥PB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将A、B两枚骰子各抛掷一次,观察向上的点数,问:
(1)共有多少种不同的结果?
(2)两枚骰子点数之和是3的倍数的结果有多少种?
(3)两枚骰子点数之和是3的倍数的概率为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=sin(2x﹣ ![]() )的图象,可以将函数y=sin2x的图象( )
)的图象,可以将函数y=sin2x的图象( )
A.向右平移 ![]() 个单位
个单位
B.向右平移 ![]() 个单位
个单位
C.向左平移 ![]() 个单位
个单位
D.向左平移 ![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O1和圆O2的极坐标方程分别为ρ=2, ![]() .
.
(1)把圆O1和圆O2的极坐标方程化为直角坐标方程;
(2)求经过两圆交点的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知直线l1:kx+y=0和直线l2:kx+y+b=0(b>0),射线OC的一个法向量为 ![]() =(﹣k,1),点O为坐标原点,且k≥0,直线l1和l2之间的距离为2,点A、B分别是直线l1、l2上的动点,P(4,2),PM⊥l1于点M,PN⊥OC于点N;
=(﹣k,1),点O为坐标原点,且k≥0,直线l1和l2之间的距离为2,点A、B分别是直线l1、l2上的动点,P(4,2),PM⊥l1于点M,PN⊥OC于点N; 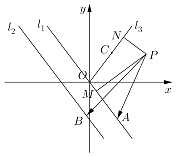
(1)若k=1,求|OM|+|ON|的值;
(2)若| ![]() |=8,求
|=8,求 ![]() 的最大值;
的最大值;
(3)若k=0,AB⊥l2 , 且Q(﹣4,﹣4),试求|PA|+|AB|+|BQ|的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com