
【题目】如图,在底面是菱形的四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
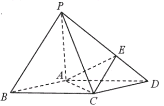
(1)证明:![]() 面
面![]() ;
;
(2)在棱![]() 上是否存在一点
上是否存在一点![]() ,使三棱锥
,使三棱锥![]() 是正三棱锥?证明你的结论.
是正三棱锥?证明你的结论.
(3)求以![]() 为棱,
为棱,![]() 与
与![]() 为面的二面角
为面的二面角![]() 的大小.
的大小.
【答案】(1)证明详见解析;(2)不存在点F,证明详见解析;(3)![]()
【解析】
(1)由已知求解三角形可知![]() ,
,![]() ,再由线面垂直判断定理证明;
,再由线面垂直判断定理证明;
(2)若三棱锥![]() 是正三棱锥,那么点
是正三棱锥,那么点![]() 在底面的射影应是正三角形
在底面的射影应是正三角形![]() 的中心,
的中心,
利用(1)的结论可知![]() 平面
平面![]() ,逐步可推得矛盾;
,逐步可推得矛盾;
(3)作![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,可证明
,可证明![]() 是
是![]() 与
与![]() 为面的二面角的平面角,再求解交的大小.
为面的二面角的平面角,再求解交的大小.
证明:底面![]() 是菱形,
是菱形,![]() ,
,
![]() ,
,
![]() 中,由
中,由![]() ,则
,则![]() ,
,
同理![]() ,
,
又![]() ,
,
![]() 平面
平面![]() ;
;
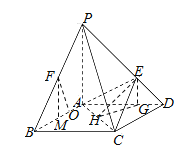
(2)在棱![]() 上不存在点
上不存在点![]() ,使三棱锥
,使三棱锥![]() 是正三棱锥,
是正三棱锥,
假设在棱![]() 上存在点
上存在点![]() ,使三棱锥
,使三棱锥![]() 是正三棱锥,过点
是正三棱锥,过点![]() 作底面
作底面![]() 的垂线,垂足为
的垂线,垂足为![]() ,则
,则![]() 为
为![]() 的中心,
的中心,
在平面![]() 内,过
内,过![]() 作
作![]() 交
交![]() 于
于![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
这样过平面![]() 外一点
外一点![]() ,有两条直线
,有两条直线![]() 与平面
与平面![]() 垂足,这与应过平面外有一条直线与平面垂直相矛盾,故假设不成立,
垂足,这与应过平面外有一条直线与平面垂直相矛盾,故假设不成立,
即在棱![]() 上不存在点
上不存在点![]() ,使三棱锥
,使三棱锥![]() 是正三棱锥.
是正三棱锥.
(3)作![]() 交
交![]() 于
于![]() ,
,
![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,![]()
![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,
![]() ,
,
![]() 平面
平面![]() ,
,![]()
![]()
![]() 是
是![]() 与
与![]() 为面的二面角的平面角,设为
为面的二面角的平面角,设为![]()
![]()
![]() ,
,![]() ,
,![]() ,
,
![]() ,即
,即![]()
所以![]() 与
与![]() 为面的二面角
为面的二面角![]() 的大小为
的大小为![]() .
.


科目:高中数学 来源: 题型:
【题目】在等腰直角三角形![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 上异于
上异于![]() 的一点,光线从点
的一点,光线从点![]() 出发,经
出发,经![]() 反射后又回到原点
反射后又回到原点![]() ,光线
,光线![]() 经过
经过![]() 的重心.
的重心.
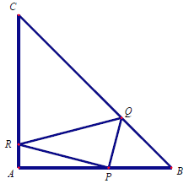
(1)建立适当的坐标系,请求![]() 的重心
的重心![]() 的坐标;
的坐标;
(2)求点![]() 的坐标;
的坐标;
(3)求![]() 的周长及面积.
的周长及面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
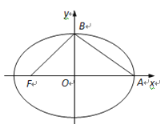
【题目】如图,在平面直角坐标系xOy中,椭圆![]()
![]() 的左焦点为
的左焦点为![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() .
.
(1)已知椭圆的离心率为![]() ,线段
,线段![]() 中点的横坐标为
中点的横坐标为![]() ,求椭圆的标准方程;
,求椭圆的标准方程;
(2)已知△![]() 外接圆的圆心在直线
外接圆的圆心在直线![]() 上,求椭圆的离心率
上,求椭圆的离心率![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某地区乡居民人民币储蓄存款(年底余额)如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
时间代号x | 1 | 2 | 3 | 4 | 5 | 6 |
储蓄存款y(千亿元) | 3.5 | 5 | 6 | 7 | 8 | 9.5 |
(1)求关于x的回归方程![]() ,并预测该地区2019年的人民币储蓄存款(用最简分数作答).
,并预测该地区2019年的人民币储蓄存款(用最简分数作答).
(2)在含有一个解释变量的线性模型中,![]() 恰好等于相关系数r的平方,当
恰好等于相关系数r的平方,当![]() 时,认为线性冋归模型是有效的,请计算
时,认为线性冋归模型是有效的,请计算![]() 并且评价模型的拟合效果(计算结果精确到0.001).
并且评价模型的拟合效果(计算结果精确到0.001).
附:
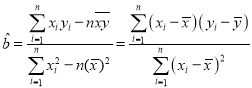 ,
,
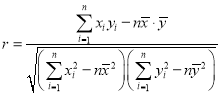
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题(1)![]() 条斜线段长相等,则他们在平面内的射影长也相等;(2)直线
条斜线段长相等,则他们在平面内的射影长也相等;(2)直线![]() 不在平面
不在平面![]() 内,他们在平面
内,他们在平面![]() 内的射影是两条平行直线,则
内的射影是两条平行直线,则![]() ;(3)与同一平面所成的角相等的两条直线平行;(4)一条直线与一个平面所成的角是
;(3)与同一平面所成的角相等的两条直线平行;(4)一条直线与一个平面所成的角是![]() ,那么它与平面内任何其他直线所成的角都不小于
,那么它与平面内任何其他直线所成的角都不小于![]() ;其中正确的命题序号是____________.
;其中正确的命题序号是____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】再直角坐标系中,定义两点![]() ,
,![]() 间的“直角距离”为
间的“直角距离”为![]() ,现有下列命题:
,现有下列命题:
①若![]() ,
,![]() 是
是![]() 轴上两点,则
轴上两点,则![]()
②已知![]() ,
,![]() ,则
,则![]() 为定值
为定值
③原点![]() 到直线
到直线![]() 上任一点
上任一点![]() 的直角距离
的直角距离![]() 的最小值为
的最小值为![]()
④设![]() 且
且![]() ,
,![]() ,若点
,若点![]() 是在过
是在过![]() 与
与![]() 的直线上,且点
的直线上,且点![]() 到点
到点![]() 与
与![]() 的“直角距离”之和等于
的“直角距离”之和等于![]() ,那么满足条件的点
,那么满足条件的点![]() 只有
只有![]() 个.
个.
其中的真命题是____________.(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个创业青年租用一块边长为4百米的等边![]() 田地
田地![]() 如图
如图![]() 养蜂、产蜜与售蜜,田地内拟修建笔直小路MN,AP,其中M,N分别为AC,BC的中点,点P在CN上,
养蜂、产蜜与售蜜,田地内拟修建笔直小路MN,AP,其中M,N分别为AC,BC的中点,点P在CN上,![]() 规划在小路MN与AP的交点O(O与M、N不重合
规划在小路MN与AP的交点O(O与M、N不重合![]() 处设立售蜜点,图中阴影部分为蜂巢区,空白部分为蜂源植物生长区,A,N为出入口
处设立售蜜点,图中阴影部分为蜂巢区,空白部分为蜂源植物生长区,A,N为出入口![]() 小路的宽度不计
小路的宽度不计![]() 为节约资金,小路MO段与OP段建便道,供蜂源植物培育之用,费用忽略不计
为节约资金,小路MO段与OP段建便道,供蜂源植物培育之用,费用忽略不计![]() 为车辆安全出入,小路AO段的建造费用为每百米5万元,小路ON段的建造费用为每百米4万元.
为车辆安全出入,小路AO段的建造费用为每百米5万元,小路ON段的建造费用为每百米4万元.
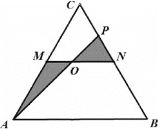
(Ⅰ)若拟修的小路AO段长为![]() 百米,求小路ON段的建造费用;
百米,求小路ON段的建造费用;
(Ⅱ)设![]() , 求
, 求![]() 的值,使得小路AO段与ON段的建造总费用最小.
的值,使得小路AO段与ON段的建造总费用最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,给出下列结论:
,给出下列结论:
①![]() 在
在![]() 上是减函数;
上是减函数;
②![]() 在
在![]() 上的最小值为
上的最小值为![]() ;
;
③![]() 在
在![]() 上至少有两个零点.
上至少有两个零点.
其中正确结论的序号为_________(写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点为F,短轴的两个端点分别为A、B,且
的左焦点为F,短轴的两个端点分别为A、B,且![]() ,
,![]() 为等边三角形.
为等边三角形.
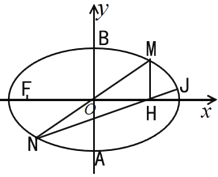
(1)求椭圆C的方程;
(2)如图,点M在椭圆C上且位于第一象限内,它关于坐标原点O的对称点为N;过点M作x轴的垂线,垂足为H,直线![]() 与椭圆C交于另一点J,若
与椭圆C交于另一点J,若![]() ,试求以线段
,试求以线段![]() 为直径的圆的方程;
为直径的圆的方程;
(3)已知![]() 是过点A的两条互相垂直的直线,直线
是过点A的两条互相垂直的直线,直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,直线
两点,直线![]() 与椭圆C交于另一点R;求
与椭圆C交于另一点R;求![]() 面积取最大值时,直线
面积取最大值时,直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com