
【题目】已知k∈R, ![]() =(k,1),
=(k,1), ![]() =(2,4),若|
=(2,4),若| ![]() |<
|< ![]() ,则△ABC是钝角三角形的概率是( )
,则△ABC是钝角三角形的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ),记
),记![]() 的导函数为
的导函数为![]() .
.
(1) 证明:当![]() 时,
时, ![]() 在
在![]() 上的单调函数;
上的单调函数;
(2)若![]() 在
在![]() 处取得极小值,求
处取得极小值,求![]() 的取值范围;
的取值范围;
(3)设函数![]() 的定义域为
的定义域为![]() ,区间
,区间![]() .若
.若![]() 在
在![]() 上是单调函数,则称
上是单调函数,则称![]() 在
在![]() 上广义单调.试证明函数
上广义单调.试证明函数![]() 在
在![]() 上广义单调.
上广义单调.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(n)是定义在N*上的增函数,f(4)=5,且满足:
①任意n∈N*,f(n)![]() Z;②任意m,n∈N*,有f(m)f(n)=f(mn)+f(m+n-1).
Z;②任意m,n∈N*,有f(m)f(n)=f(mn)+f(m+n-1).
(1)求f(1),f(2),f(3)的值;
(2)求f(n)的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心(a,b)(a<0,b<0)在直线y=2x+1上的圆,若其圆心到x轴的距离恰好等于圆的半径,在y轴上截得的弦长为 ![]() ,则圆的方程为( )
,则圆的方程为( )
A.(x+2)2+(y+3)2=9
B.(x+3)2+(y+5)2=25
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对两个变量y和x进行回归分析,得到一组样本数据:(x1 , y1),(x2 , y2),…,(xn , yn),则下列说法中不正确的是( )
A.由样本数据得到的回归方程 ![]() =
= ![]() x+
x+ ![]() 必过样本中心(
必过样本中心( ![]() ,
, ![]() )
)
B.残差平方和越小的模型,拟合的效果越好
C.用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好
D.两个随机变量的线性相关性越强,相关系数的绝对值越接近于1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子中装有5张编号依次为1,2,3,4,5的卡片,这5张卡片除号码外完全相同,现进行有放回的连续抽取两次,每次任意地取出一张卡片.
(1)求出所有可能结果数,并列出所有可能结果;
(2)求条件“取出卡片的号码之和不小于7或小于5”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
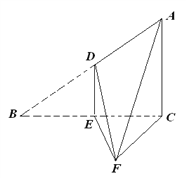
【题目】如图,直角![]() 中,∠
中,∠![]() ,
,![]() ,D、E分别是AB、BC边的中点,沿DE将
,D、E分别是AB、BC边的中点,沿DE将![]() 折起至
折起至![]() ,且∠
,且∠![]() .
.
(Ⅰ)求四棱锥F-ADEC的体积;
(Ⅱ)求证:平面ADF⊥平面ACF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1、F2分别是双曲线 ![]() 的左右焦点,A为双曲线的右顶点,线段AF2的垂直平分线交双曲线与P,且|PF1|=3|PF2|,则该双曲线的离心率是( )
的左右焦点,A为双曲线的右顶点,线段AF2的垂直平分线交双曲线与P,且|PF1|=3|PF2|,则该双曲线的离心率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题中其中真命题个数是( )
①为了了解800名学生的成绩,打算从中抽取一个容量为40的样本,考虑用系统抽样,则分段的间隔k为40;
②线性回归直线![]() 恒过样本点的中心
恒过样本点的中心![]() ;
;
③随机变量ξ服从正态分布N(2,σ2)(σ>0),若在(﹣∞,1)内取值的概率为0.1,则在(2,3)内的概率为0.4;
④若事件![]() 和
和![]() 满足关系
满足关系![]() ,则事件
,则事件![]() 和
和![]() 互斥.
互斥.
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com