
【题目】已知函数![]() ,
,![]() 且
且![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若![]() ,求证:函数
,求证:函数![]() 有且只有一个零点.
有且只有一个零点.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)通过导函数![]() 当
当![]() 和
和![]() 时的正负来确定原函数的增减区间;
时的正负来确定原函数的增减区间;
(2) 通过证明函数单调并且猜出函数的一个根,从而证明函数有且只有一个零点.
试题解析:
(1)![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,由
时,由![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
即![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增.
上单调递增.
(2)证明:由已知得![]() ,则
,则![]() ,
,
设![]() ,则
,则![]()
![]() ,
,
故![]() 为
为![]() 上的增函数,
上的增函数,
又由于![]() ,因此
,因此![]() 且
且![]() 有唯一零点1,
有唯一零点1,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,
上为增函数,
![]() 函数
函数![]() 有且只有一个零点.
有且只有一个零点.
点晴:本题主要考查导数在解决函数中的应用. 解答此类问题,应该首先确定函数的定义域,否则,写出的单调区间易出错. 解决含参数问题及不等式问题注意两个转化:(1)利用导数解决含有参数的单调性问题可将问题转化为含参不等式的求解问题,要注意分类讨论和数形结合思想的应用.(2)函数有且只有一个零点通常是证明函数单调并且猜出函数的一个根,从而证明函数有且只有一个零点.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() sinωx·cosωx-cos2ωx(ω>0)的最小正周期为
sinωx·cosωx-cos2ωx(ω>0)的最小正周期为![]() .
.
(1)求ω的值;
(2)在△ABC中,sinB,sinA,sinC成等比数列,求此时f(A)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题中错误的是( )
A. 在一次试卷分析中,从每个考室中抽取第5号考生的成绩进行统计,不是简单随机抽样
B. 对一个样本容量为100的数据分组,各组的频数如下:
区间 |
|
|
|
|
|
|
|
|
频数 | 1 | 1 | 3 | 3 | 18 | 16 | 28 | 30 |
估计小于29的数据大约占总体的![]()
C. 设产品产量与产品质量之间的线性相关系数为![]() ,这说明二者存在着高度相关
,这说明二者存在着高度相关
D. 通过随机询问110名性别不同的行人,对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查,得到如表列联表.

由![]() ,则有
,则有![]() 以上的把握认为“选择过马路方式与性别有关”
以上的把握认为“选择过马路方式与性别有关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】统计表明,某种型号的汽车在匀速行驶中每小时耗油量![]() (升)关于行驶速度
(升)关于行驶速度![]() (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为: ![]() ,已知甲、乙两地相距100千米.
,已知甲、乙两地相距100千米.
(1)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】调查在![]() 级风的海上航行中71名乘客的晕船情况,在男人中有12人晕船,25人不晕船,在女人中有10人晕船,24人不晕船
级风的海上航行中71名乘客的晕船情况,在男人中有12人晕船,25人不晕船,在女人中有10人晕船,24人不晕船
(1)作出性别与晕船关系的列联表;
(2)根据此资料,能否在犯错误的概率不超过0.1的前提下认为![]() 级风的海上航行中晕船与性别有关?
级风的海上航行中晕船与性别有关?
晕船 | 不晕船 | 总计 | |
男人 | |||
女人 | |||
总计 |
附:.![]()
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位为绿化环境,移栽了甲、乙两种大树各2株.设甲、乙两种大树移栽的成活率分别为![]() 和
和![]() ,且各株大树是否成活互不影响.求移栽的4株大树中:
,且各株大树是否成活互不影响.求移栽的4株大树中:
(1)两种大树各成活1株的概率;
(2)成活的株数ξ的分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
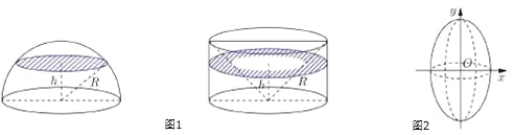
【题目】(数学文卷·2017届重庆十一中高三12月月考第16题) 现介绍祖暅原理求球体体积公式的做法:可构造一个底面半径和高都与球半径相等的圆柱,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥,用这样一个几何体与半球应用祖暅原理(图1),即可求得球的体积公式.请研究和理解球的体积公式求法的基础上,解答以下问题:已知椭圆的标准方程为![]() ,将此椭圆绕y轴旋转一周后,得一橄榄状的几何体(图2),其体积等于______.
,将此椭圆绕y轴旋转一周后,得一橄榄状的几何体(图2),其体积等于______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com