
【题目】作家马伯庸小说《长安十二时辰》中,靖安司通过长安城内的望楼传递信息.同名改编电视剧中,望楼传递信息的方式有一种如下:如图所示,在九宫格中,每个小方格可以在白色和紫色(此处以阴影代表紫色)之间变换,从而一共可以有512种不同的颜色组合,即代表512种不同的信息.现要求每一行,每一列上至多有一个紫色小方格(如图所示即满足要求).则一共可以传递______种信息.(用数字作答)

 互动英语系列答案
互动英语系列答案科目:高中数学 来源: 题型:
【题目】某省开展“精准脱贫,携手同行”的主题活动,某贫困县统计了100名基层干部走访贫困户的数量,并将走访数量分成5组,统计结果见下表.
走访数量区间 | 频数 | 频率 |
| b | |
| 10 | |
| 38 | |
| a | 0.27 |
| 9 | |
总计 | 100 | 1.00 |
(1)求a与b的值;
(2)根据表中数据,估计这100名基层干部走访数量的中位数(精确到个位);
(3)如果把走访贫困户不少于35户视为“工作出色”,按照分层抽样,从“工作出色”的基层干部中抽取4人,再从这4人中随机抽取2人,求其中有1人走访贫困户不少于45户的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设中心在原点,焦点在![]() 轴上的椭圆
轴上的椭圆![]() 过点
过点![]() ,且离心率为
,且离心率为![]() .
.![]() 为
为![]() 的右焦点,
的右焦点,![]() 为
为![]() 上一点,
上一点,![]() 轴,
轴,![]() 的半径为
的半径为![]() .
.
(1)求![]() 和
和![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 交于
交于![]() 两点,与
两点,与![]() 交于
交于![]() 两点,其中
两点,其中![]() 在第一象限,是否存在
在第一象限,是否存在![]() 使
使![]() ?若存在,求
?若存在,求![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() :
:![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 的面积为1,
的面积为1,![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 是椭圆
是椭圆![]() 上一点,
上一点,![]() 、
、![]() 是椭圆的左右两个焦点,直线
是椭圆的左右两个焦点,直线![]() 、
、![]() 分别交
分别交![]() 于
于![]() 、
、![]() ,是否存在点
,是否存在点![]() ,使
,使![]() ,若存在,求出
,若存在,求出![]() 点的横坐标;若不存在,请说明理由.
点的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,上顶点为A,过
,上顶点为A,过![]() 的直线
的直线![]() 与y轴交于点M,满足
与y轴交于点M,满足![]() (O为坐标原点),且直线l与直线
(O为坐标原点),且直线l与直线![]() 之间的距离为
之间的距离为![]() .
.
(1)求椭圆C的方程;
(2)在直线![]() 上是否存在点P,满足
上是否存在点P,满足![]() ?存在,指出有几个这样的点(不必求出点的坐标);若不存在,请说明理由.
?存在,指出有几个这样的点(不必求出点的坐标);若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】华为手机作为全球手机销量第二位,一直深受消费者喜欢.据调查数据显示,2019年度华为手机(含荣耀)在中国市场占有率接近![]() !小明为了考查购买新手机时选择华为是否与年龄有一定关系,于是随机调查100个2019年购买新手机的人,得到如下不完整的列表.定义30岁以下为“年轻用户”,30岁以上为“非年轻用户”.
!小明为了考查购买新手机时选择华为是否与年龄有一定关系,于是随机调查100个2019年购买新手机的人,得到如下不完整的列表.定义30岁以下为“年轻用户”,30岁以上为“非年轻用户”.
购买华为 | 购买其他 | 总计 | |
年轻用户 | 28 | ||
非年轻用户 | 24 | 60 | |
总计 |
附: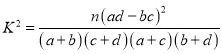 .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
(1)将列表填充完整,并判断是否有![]() 的把握认为购买手机时选择华为与年龄有关?
的把握认为购买手机时选择华为与年龄有关?
(2)若采用分层抽样的方法从购买华为手机用户中抽出6个人,再随机抽2人,求恰好抽到的两人都是非年轻用户的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二面角P﹣AB﹣C的大小为120°,且∠PAB=∠ABC=90°,AB=AP,AB+BC=6.若点P,A,B,C都在同一个球面上,则该球的表面积的最小值为( )
A.45πB.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (
(![]() 为自然对数的底数,
为自然对数的底数,![]() ).
).
(1)当![]() 时,求函数
时,求函数![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在区间
在区间![]() 上具有单调性,求
上具有单调性,求![]() 的取值范围;
的取值范围;
(3)若函数![]()
![]() 有且仅有
有且仅有![]() 个不同的零点
个不同的零点![]() ,且
,且![]() ,
,![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】欧阳修《卖油翁》中写道:(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌滴沥之,自钱孔入,而钱不湿.已知铜钱是直径为4 cm的圆面,中间有边长为1 cm的正方形孔,若随机向铜钱上滴一滴油(油滴整体落在铜钱内),则油滴整体(油滴是直径为0.2 cm的球)正好落入孔中的概率是_____.(不作近似计算)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com