
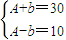 ,从而可求得A,b,再有函数图象可知其周期为16,从而可求得ω,进一步可求得φ,于是可求得这段曲线的函数解析式;
,从而可求得A,b,再有函数图象可知其周期为16,从而可求得ω,进一步可求得φ,于是可求得这段曲线的函数解析式; x+
x+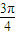 )≤
)≤ ,结合正弦函数的图象与性质有2kπ≤
,结合正弦函数的图象与性质有2kπ≤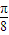 x+
x+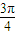 ≤2kπ+
≤2kπ+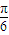 ,或2kπ+
,或2kπ+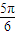 ≤
≤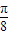 x+
x+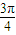 ≤2kπ+π,分别对k赋值即可求得答案.
≤2kπ+π,分别对k赋值即可求得答案.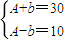 解得
解得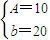 ,
, ×
×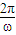 =14-6,所以ω=
=14-6,所以ω=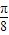 ,
,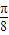 x+φ)+20;
x+φ)+20;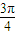 .
.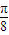 x+
x+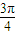 )+20.…(6分)
)+20.…(6分)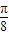 x+
x+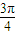 )+20≤25,
)+20≤25,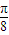 x+
x+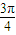 )≤
)≤ .
.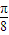 x+
x+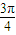 ≤2kπ+
≤2kπ+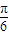 ,…①
,…①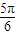 ≤
≤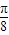 x+
x+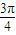 ≤2kπ+π,…②
≤2kπ+π,…② .取k=1,得10≤x≤11+
.取k=1,得10≤x≤11+ .
. ≤x≤16k+2.取k=0,得
≤x≤16k+2.取k=0,得 ≤x≤2;
≤x≤2; ≤x≤18.
≤x≤18.

科目:高中数学 来源: 题型:
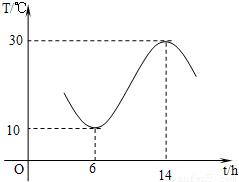
 (2012•武昌区模拟)武汉地区春天的温度的变化曲线近似地满足函数y=Asin(ωx+φ)+b(如图所示,单位:摄氏温度,A>0,ω>0,0<φ<π).
(2012•武昌区模拟)武汉地区春天的温度的变化曲线近似地满足函数y=Asin(ωx+φ)+b(如图所示,单位:摄氏温度,A>0,ω>0,0<φ<π).查看答案和解析>>
科目:高中数学 来源:湖北省武汉市武昌区2012届高三5月调研考试数学文科试题 题型:044
武汉地区春天的温度的变化曲线近似地满足函数y=Asin(ωx+φ)+b(如图所示,单位:摄氏温度,A>0,ω>0,0<φ<π).
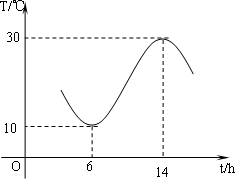
(Ⅰ)写出这段曲线的函数解析式;
(Ⅱ)求出一天(t∈[0,24],单位小时)温度的变化在[20,25]时的时间.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
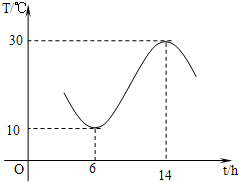 武汉地区春天的温度的变化曲线近似地满足函数y=Asin(ωx+φ)+b(如图所示,单位:摄氏温度,A>0,ω>0,0<φ<π).
武汉地区春天的温度的变化曲线近似地满足函数y=Asin(ωx+φ)+b(如图所示,单位:摄氏温度,A>0,ω>0,0<φ<π).查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖北省武汉市武昌区高三5月调研考试文科数学试卷(解析版) 题型:解答题
(本题满分12分)(课本必修4第60页例1改编)
武汉地区春天的温度的变化曲线近似地满足函数 (如图所示,单位:摄氏温度,
(如图所示,单位:摄氏温度, ).
).

(Ⅰ)写出这段曲线的函数解析式;
(Ⅱ)求出一天( ,单位小时)
,单位小时)
温度的变化在 时的时间.
时的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com