
【题目】在平面直角坐标系xOy中,以原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知点A的极坐标为( ![]() ,
, ![]() ),直线l的极坐标方程为ρcos(θ﹣
),直线l的极坐标方程为ρcos(θ﹣ ![]() )=a,且点A在直线l上.
)=a,且点A在直线l上.
(1)求a的值及直线l的直角坐标方程;
(2)若圆C的参数方程为 ![]() (α为参数),试判断直线l与圆C的位置关系.
(α为参数),试判断直线l与圆C的位置关系.
【答案】
(1)解:点A的极坐标为( ![]() ,
, ![]() ),直线l的极坐标方程为ρcos(θ﹣
),直线l的极坐标方程为ρcos(θ﹣ ![]() )=a,且点A在直线l上.
)=a,且点A在直线l上.
可得: ![]() cos(
cos( ![]() ﹣
﹣ ![]() )=a,解得a=
)=a,解得a= ![]() .
.
直线l的极坐标方程为ρcos(θ﹣ ![]() )=
)= ![]() ,即:ρcosθ+ρsinθ=2,
,即:ρcosθ+ρsinθ=2,
直线l的直角坐标方程为:x+y﹣2=0
(2)解:圆C的参数方程为 ![]() (α为参数),可得圆的直角坐标方程为:(x﹣1)2+y2=1.
(α为参数),可得圆的直角坐标方程为:(x﹣1)2+y2=1.
圆心(1,0),半径为:1.
因为圆心到直线的距离d= ![]() =
= ![]() <1,
<1,
所以直线与圆相交
【解析】(1)利用点在直线上,代入方程求出a,利用极坐标与直角坐标的互化,求出直线的直角坐标方程.(2)化简圆的参数方程与直角坐标方程,求出圆心与半径,利用圆心到直线的距离与半径比较即可得到直线与圆的位置关系.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AE:EB=1:2. 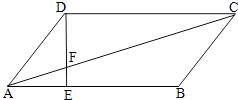
(1)求△AEF与△CDF的周长比;
(2)如果△AEF的面积等于6cm2 , 求△CDF的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的焦距为2,过短轴的一个端点与两个焦点的圆的面积为
的焦距为2,过短轴的一个端点与两个焦点的圆的面积为![]() ,过椭圆
,过椭圆![]() 的右焦点作斜率为
的右焦点作斜率为![]() (
(![]() )的直线
)的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 垂直于
垂直于![]() 的直线与
的直线与![]() 轴交于点
轴交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P(1,m)在抛物线C:y2=2Px(P>0)上,F为焦点,且|PF|=3.
(1)求抛物线C的方程;
(2)过点T(4,0)的直线l交抛物线C于A,B两点,O为坐标原点.
(ⅰ)求 ![]() 的值;
的值;
(ⅱ)若以A为圆心,|AT|为半径的圆与y轴交于M,N两点,求△MNF的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
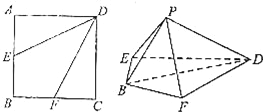
如图,在正方形ABCD中,点E,F分别是AB,BC的中点.将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于P.
(1)求证:平面PBD⊥平面BFDE;
(2)求二面角P﹣DE﹣F的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班有36名同学参加数学、物理、化学课外探究小组,每名同学至多参加两个小组,已知参加数学、物理、化学小组的人数分别为26,15,13,同时参加数学和物理小组的有6人,同时参加物理和化学小组的有4人,则同时参加数学和化学小组的有人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设小明家订了一份报纸,送报人可能在早上6:30﹣7:30之间把报纸送到小明家,小明父亲离开家去工作的时间在早上7:00﹣8:00之间,问小明父亲在离开家前能得到报纸(称为事件A)的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com